Aurélie 06 /02
charge, décharge d'un condensateur

suite --> ressort (concours Geipi 02)

Google

Charge et décharge d'un condensateur

On considère le montage ci-dessous. Le condensateur a une capacité de C=2mF , la résistance R1 vaut 500 kW et la résistance R2 vaut 1 MW . Le générateur de tension continue a une f.e.m. E de 10 V.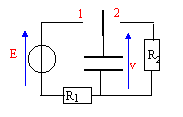

  1. Calculer la constante de temps du dipôle R1C.
  2. A l'instant t = 0 , on bascule l'inverseur en position 1. Déterminer à t = 10 s :
    - La valeur de la tension V aux bornes du condensateur.
    - L'intensité du courant I circulant dans le circuit.
  3. A l'instant t = 20 s , on bascule l'inverseur en position 2. Déterminer la valeur de la tension V aux bornes du condensateur à t = 22 s.

Charge d'un condensateur à courant constant

Le même condensateur initialement non chargé, est chargé à présent par un générateur de courant constant de 1 mA. A l'instant t = 0 , on ferme l'interrupteur K.

  1. Déterminer l'instant t1 auquel la tension aux bornes du condensateur atteint 10 V.
  2. Déterminer l'instant t2 auquel l'énergie emmagasinée dans le condensateur est égale à 1 mJ.
 

corrigé
t = R1C = 500 103* 210-6 = 1 s.

la charge est terminée au dela de cinq fois la constante de temps soit 5s. Donc à t= 10s la tension aux bornes du condensateur est égale à E = 10V et l'intensité du courant dans le circuit est nulle.

constante de temps du dipole R2C : 106* 210-6 = 2 s.

à t = 22 s, la décharge du condensateur dure depuis 2s soit une fois la constante de temps.

la tension aux bornes du condensateur qui se décharge a diminué de 63% fois sa valeur maximale soit 10*0,63 =6,3V

il reste donc V= 10-6,3 = 3,7 V.

charge à l'aide d'un générateur de courant :

charge q = i t

tension aux bornes du condensateur v = q / C = i / C t = 10-3 / 2 10-6 t = 500 t

t1 =10 /500 = 0,02 s.

énergie E = ½ q² / C = 0,5 i² t² / C = 0,5 * 10-6 / 2 10-6 t² = 0,25 t²

t2 = racine carrée (E/0,25) = racine carrée (10-3/0,25) = 6,3 10-2 s = 63 ms.

retour - menu