Aurélie 06 /02
ressort

concours Geipi 02

Google

Soit un ressort de raideur k , de longueur au repos l0 , de masse négligeable. L'extrémité inférieure A du ressort est fixe. Sur l'extrémité supérieure B est fixe un plateau de masse M. (L'axe du ressort est vertical). Soit (Oz) un axe vertical ascendant.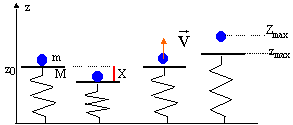
- a. On place sur le plateau une masse ponctuelle m . On appelle z0, la cote " au repos " de la masse m ainsi placée (situation dite " au repos ").
- b. On comprime le ressort d'une quantité X (on amène la masse m et le dessus du plateau à la cote z0 -X.
- c. On lâche le système : on admet que la masse m et le plateau restent liés tant que z , cote de la masse m est inférieure ou égale à z0, on admet que la masse m et le plateau se séparent dès que z , cote de la masse m est supérieure à z0.
- d. On désigne par V, la vitesse de la masse m et du plateau, lorsque la cote z = z0 est atteinte ; on désigne par zmax la cote maximale atteinte par la masse m et par Zmax, la cote maximale atteinte par le plateau M.

Les questions suivantes sont indépendantes.

  1. A partir du bilan des forces dans la situation en (a), exprimer k(z0-l0) en fonction de m, M, g.
  2. A partir de la conservation de l'énergie entre b et c , pour le système constitué de m et M, écrire l'équation permettant le calcul de V.
  3. Simplifier l'expression précédente en tenant compte de l'équation trouvée en (1) et exprimer V en fonction de k, m, M et X.
  4. A partir de la conservation de l'énergie pour le système m , exprimer la cote Zmax atteinte par la masse m en fonction de V.
  5. A partir de la conservation de l'énergie pour le système constitué du plateau et du ressort, écrire l'équation permettant le calcul de la cote zmax atteinte par le plateau . 

corrigé
Dans la situation en (a) :
L'extrémité supérieure du ressort est soumise à trois forces verticales qui se neutralisent : poids du plateau et poids de la masse m, verticale vers le bas; tension du ressort verticale vers le haut.

Mg + mg = k(l0-z0) (1)

On choisit comme origine de l'énergie potentielle de pesanteur et comme origine de l'énergie potentielle élastique la position du ressort dans la position d'équilibre ( situation a).

Dans la situation en (b) :

L'énergie du système {ressort, plateau, masse m} est sous forme potentielle élastique et de pesanteur, la longueur du ressort étant z0-X, l'altitude du centre d'inertie de la masse et du plateau étant -X.

Em = ½k ( z0-X-l0)² + (M+m)g(-X)

Dans la situation en (c) :

l'énergie de ce système est sous forme cinétique :

Em = ½(M+m) V²

l'énergie mécanique se conserve :

½k ( z0-l0-X)² - (M+m)g X = ½(M+m) V²

V² =k ( z0-l0-X)² / (M+m)-2gX

Zmax atteinte par la masse m en fonction de V :
on considère uniquement la masse m :

énergie mécanique juste avant décollage : ½mV².

énergie mécanique au point le plus haut ( vitesse nulle) = énergie potentielle de pesanteur = mg Zmax.

conservation de l'énergie mécanique : ½mV² = mgZmax

Zmax =½ V² / g.

zmax atteinte par le plateau : 
le système étudié est le plateau de masse M :

énergie mécanique à l'instant où la masse m décolle : ½MV².

énergie mécanique au point le plus haut (vitesse nulle) : ½k(zmax-l0)²+Mg(zmax-z0).

conservation de l'énergie mécanique :

½MV² = ½k(zmax-l0)²+ Mg(zmax-z0).

retour - menu