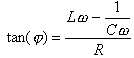. .
courant alternatif (sup) dipole RC, RL (lycée) dipole RLC libre ou forcé (lycée) fiche de révisions (quiz) nombres complexes et électricité (sup)
rappels	en régime sinusoïdal
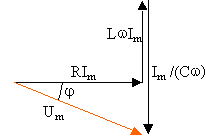
grandeur physique nombre complexe associé quelques règles intensité Imcos(wt) Im Aux impédances complexes les lois du courant continu s'appliquent. tension Umcos(wt+j) Umejj impédance (inductance) jLw en série elles s'ajoutent en dérivation les admittances (inverse d'une impédance) s'ajoutent impédance (capacité) -j / (Cw) impédance (résistance) R loi d'ohm u = Z i toute lettre soulignée est un nombre complexe impédance réelle = module de l'impédance complexe. arg u = arg Z +arg i dériver c'est multiplier par jw intégrer c'est diviser par jw
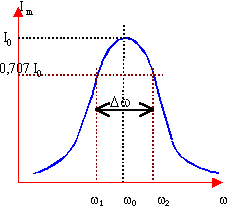
cours	circuit RLC série en régime forcé
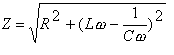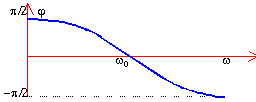
impédance complexe R+j(Lw-1/ (Cw) représentation vectorielle impédance réelle Lw-1/Cw :réactance la phase de i est l'origine des phases résonance d'intensité : l'intensité passe par une valeur maximale si l'impédance Z est minimale ègale à R LCwo²=1 facteur de qualité ou de surtension Q=Lwo / R bande passante Dw =wo / Q
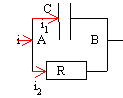
exercice 1	circuits équivalents à un condensateur réel
UAB efficace =200 V ; C=20nF; le courant est en avance sur la tension de j=85 ° . (w=500 rad s-1) Le condensateur présente une résistance de fuite R que l'on demande de calculer. Expliciter l'intensité i du courant dans le circuit. On veut remplacer le groupement précédent par un condensateur C' en série avec R'. Calculer C' et R'
..
corrigé
impédance complexe z équivalente : 1/z = 1/R+ jCw ; z=R/(1+(RCw)²)(1-jRCw) impédance réelle Z=R/rac carrée(1+R²C²w²) phase j : tanj= -RCw en prenant la phase de i comme origine : tension en retard sur i applications numériques : R= tan(85) / (2 10-8*500)= 1,14 MW Z=105 W ; Ieff= Ueff / Z = 200/105= 2 mA i=2,8 sin(500 t +1,42) ; 85°=1,42 rad méthode : égaler les impédances complexes. égaler parties réelles et parties imaginaires C'=(1+R²C²w²)/ (R²C²w²) * C = 20,1 nF R'=R/ (1+R²C²w²)= 8,7 kW
exercice 2	condensateur et bobine en dérivation
On maintient une tension alternative Ueff=1 V , de pulsation w=15000 rads-1 aux bornes d'une self pure de valeur L=1 mH. Quelle capacité C0faut-il monter en dérivation aux bornes de la self pour que l'intensité soit nulle dans le circuit principal ?
.
corrigé
impédance complexe z équivalente : 1/z = 1/(jLw)+ jCw ; z=jLw/(1-LCw²) impédance réelle Z=Lw/(1-LCw²) phase j : j= p/2 car z complexe pur L'intensité est nulle lorsque Z tend vers l'infini soit LCw²=1 application numérique :C0=4,44 mF
exercice 3	self pure et résistance en dérivation
On maintient une tension alternative Ueff=200 V , de pulsation w=500 rads-1 aux bornes d'une self pure de valeur L=1 mH shuntée par une résistance R. La réactance de ce circuit est alors la moitié de ce qu'elle serait si la self était seule. Calculer R et l'intensité du courant principal.
..
corrigé
impédance complexe z équivalente : 1/z = 1/(jLw)+ 1/R ; z=RLw/(R²+L²w²)*(Lw+jR) réactance du circuit R²Lw/(R²+L²w²) partie imaginaire réactance d'une self pure Lw 0,5 Lw = R²Lw/(R²+L²w²) d'où R= Lw= 500W. intensité principale (remplacer R par Lw) l'impédance complexe z devient :0,5Lw(1+j) impédance réelle Z=353,5W phase j : j= p/4 en prenant la phase de i comme origine : tension en avance sur i Ieff=Ueff/Z =200/353,5= 0,56 A
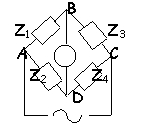
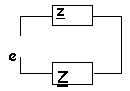
exercice 4	condition d'équilibre d'un pont de Wheatstone
On considère le pont en alternatif; entre B et D se trouve un détecteur de zéro(oscilloscope).Etablir la condition d'équilibre du pont.
.
corrigé
UAB = Z1 i1 ; UAD = Z2 i2 ; UBC = Z3 i3 ; UDC = Z4 i4 grandeurs complexes Lorsque le pont est équilibré UBD=0 donc UAB = UAD et UBC = UDC i1 = i3 et i2 = i4 la condition d'équilibre s'écrit : Z1 Z4 =Z2 Z3 elle correspond à deux conditions entre nombres réels
exercice 5	circuits couplés
M est l'inductance mutuelle. le générateur délivre une tension e1=E1cos(wt). Montrer que l'on peut remplacer ces circuit par le circuit unique dont on déterminera l'inductance L et la résistance R .
corrigé
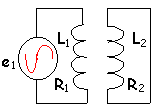
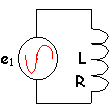
i1 et i2 intensités instantanée dans les circuits e1= L1 i'1+ Mi'2+ R1i1 et 0= L2 i'2+ Mi'1+ R2i2 en notation complexe e1= L1 jwi1 + Mjwi2 + R1i1 0= L2 jwi2 + Mjwi1+ R2i2 éliminer i2 regrouper partie réelle et partie imaginaire R= R1+M²w²R2/(R2²+(L2w2)²) L= L1+M²w²L2/(R2²+(L2w2)²)
exercice 6	puissance active
Aux bornes d'un générateur sinusoidal délivrant la tension e=Emcos(wt) d'impédance interne z=r+jx , on branche une impédance Z=R+jX. Déterminer Z pour que la puissance dissipée dans Z soit maximale .
..
corrigé
loi d'Ohm entre grandeurs complexes i = e / (z + Z) puissance active dissipée dans Z : P=RI²eff I²eff=E² / ((R+r)²+(X+x)²) La puissance est maximale lorsque les dérivées partielles de P par rapport à R et X sont nulles. on en déduit : X=-x et R=r ou Z = z* Pmax= E²/(4r)
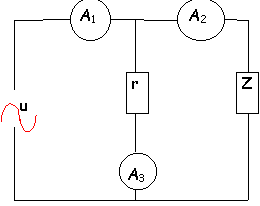
exercice 7	mesure de puissance , méthode des 3 ampèremètres
r est une résistance morte. Les résistances des ampèremètres sont négligeables. Exprimer la puissance dissipée dans Z en fonction de r et des intensités efficaces I1,I2,I3 mesurées.
.
corrigé
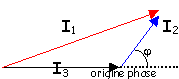
U tension efficace aux bornes de Z cos j facteur de puissance de Z P=UI2cosj. or U=rI3 et u et i3 sont en phase donc P=rI3I2cosj. I1²=I2²+I3²-2I2I3cos(p-j) cos(j)=(I1²-I2²-I3²) / (2I2I3) P = 0,5 r(I1²-I2²-I3²)
..
exercice 8	association mixte bobine condensateur résistor
C=125 mF; R1 variable; w=400rads-1.
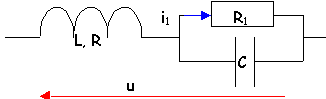
Exprimer l'impédance complexe du circuit. Exprimer l'intensité complexe i1. Quelles conditions doivent satisfaire les données pour que i1 soit indépendant de R1.
..
corrigé
impédance complexe bobine : jLw + R C et R1 en dérivation : R/ (1+jCRw) circuit : jLw + R + R1/ (1+jCR1w) intensité i1 complexe intensité principale : i = u / [ jLw + R + R1/ (1+jCR1w) ] i1 R1 = i2/(jCw) et i = i1 + i2 i1 = i / [(1+jCR1w)] = u /[(jLw + R)(1+jCR1w)+R1] l'intensité dans R1 est indépendante de R1 si le coefficient de R1 est nul soit: 1-LCw²+jRCw=0 le terme réel doit être nul :LCw² =1 le terme imaginaire doit être nul :RCw=0 ou R=0 pratiquement R=0,1W.
Puissance moyenne consommée par un dipôle Soit u= U 2½ cos (wt) la tension instantanée à la date t aux bornes d'un dipôle électrique ; U est la tension efficace, w est la pulsation de la tension. L'intensité du courant qui le traverse est i= I 2½ cos(wt+j) ; I est l'intensité efficace, j le déphasage. Exprimer la puissance instantanée p consommée par le dipôle. Exprimer la puissance moyenne P en fonction des paramètres U, I et j. Application au relèvement d’un facteur de puissance : Dans cette partie les grandeurs complexes sont soulignées et on utilise le nombre complexe j telle que j2=-1. Un moteur de puissance totale P=10 kW est alimenté sous une tension sinusoïdale de valeur efficace U=220 V et de fréquence 50 Hz. Le facteur de puissance est : cos j = 0,7. - Calculer l’intensité efficace I d’alimentation du moteur. - L’admittance complexe Y du moteur s’écrit : Y =| Y | e-j j. Exprimer simplement l’admittance réelle | Y | en fonction de I et de U. - On place un condensateur de capacité C, telle que l’association {condensateur+moteur} soit purement résistive. Comment faut-il le placer pour que le moteur continue à fonctionner normalement ? - Exprimer l’admittance complexe Yt de l’association en fonction de C,w et Y . En déduire la valeur de C. - Quelle est la propriété de la puissance moyenne consommée par le condensateur ? En déduire simplement la valeur de l’intensité efficace It d’alimentation de l’association. corrigé puissance instantanée p consommée par le dipôle : p= u i = 2UI cos (wt)cos(wt+j) p = UI (cos ( 2wt+j) + cos j) puissance moyenne P : 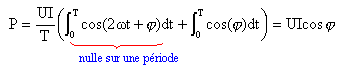P= UI cos j soit I= P/(U cosj)= 104 / (220*0,7) =64,9 A. admittance = inverse d'une impédance ; | Y | = I/U = 64,9 / 220 = 0,295 S. condensateur et moteur sont montés en dérivation : les admittances du moteur et du condensateur ( jCw) s'ajoutent. Yt=Y + jCw= | Y | e-j j + jCw. l’association {condensateur+moteur} étant purement résistive, Yt= est un nombre réel ; sa partie imaginaire est donc nulle. Yt = | Y | cosj -j | Y |sinj +jCw ; -j ; -j|Y |sinj +jCw=0 ; C= |Y |sinj/ w. avec w = 2 pf = 2*3,14*50 = 314 rad/s ; sinj= 0,714 ; |Y | =0,295 S C= 0,295*0,714 / 314 = 6,7 10-4 F. la puissance moyenne consommée par le condensateur est nulle. P active totale = P active moteur = 10 kW Q réactive totale = Q réactive condensateur = -CwU² = -6,7 10-4*314*220²= -10,2 var S²= P²+Q² = 10²+10,2²= 204,1 ; S= 14,3 VA Or S=UI soit I= 14,3 103/ 220 = 65 A.
retour - menu - menu