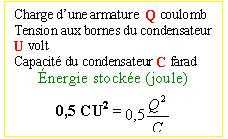|
exercice
1
|
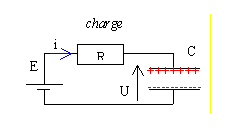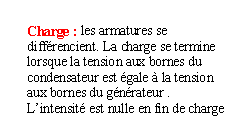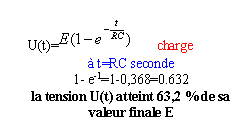
charge
d'un condensateur à l'aide d'un courant
constant
|
|
Un condensateur, de capacité 3mF, a
été chargeé par un courant
constant de 2 mA pendant
2,5 minutes. La tension aux bornes de ce
condensateur est alors de 1V ; 0,1 V ; 10 V ; 1,66
V ; 10 mV
|
corrigé
|
|
La charge de l'armature positive du
condensateur est:2
10-6
*2,5*60
=3
10-4 coulombs
La tension aux bornes du
condensateur et la charge sont proportionnelles
Q=C*U
tension=3
10-4 /
3
10-3=0,1
V
|
|
|
|
exercice
2
|
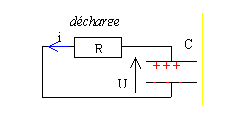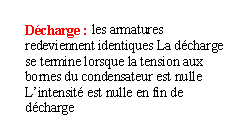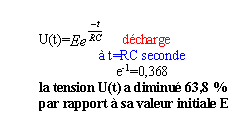
décharge
d'un condensateur à travers un
résistor
|
On donne R=1000 W
- Quelques secondes après le
début de la décharge , la
tension aux bornes du condensateur est
nulle
- Le condensateur a été
chargé à partir d'un
génrateur de tension de fem égale
à 6 V
- La constante de temps du circuit est
égale à 1 ms et la capacité
du condensateur est égale à
1mF
- Pour obtenir la même constante de
temps, en doublant la valeur de R, il faut
doubler également la valeur de C.
|
|
corrigé
|
|
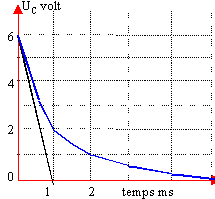
vrai
la durée de la décharge est de
l'ordre de 5 fois la constante de temps du dipole
RC soit au dela de 5 ms.
vrai
au tout début de la décharge,
la tension aux bornes du condensateur est
égale à la fem du
générateur de tension utilisé
pour la charge soit 6V.
vrai
la tangente à la date t=0 à la
courbe dessinée ci dessus coupe l'axe des
abscisses à une date égale à
la constante de temps du dipole RC
faux
en doublant R il faut diviser la
capacité par deux pour avoir la même
constante de temps voir
formule ci contre
|
t
=RC
|
|
|
|
exercice
3
|
identifier
un dipole
|
|
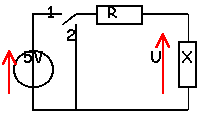
A la date t=0 on ferme
l'interrupteur en position 1. A la date
t1 l'interrupteur bascule en position 2.
A la date t2 l'interrupteur bascule en
position 1 et ainsi de suite.
- On relève la
courbe donnant la tension U aux bornes du dipole
inconnu X au cours du temps. Identifier X et
calculer la constante de temps du
circuit.
Si R=1000 ohms en
déduire la grandeur caractéristique
du dipole X.
|
|
|
corrigé
|
|
|
|
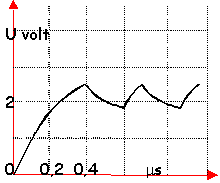
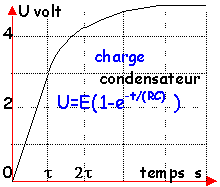
L'allure des courbes entre 0 et
t1 indique que X est un condensateur en
train de se charger.
A t=0,4 ms U=2,5 V
lecture
graphe
2,5=5(1-e-0,4/t)
avec
t=RC
en
microsecondes
2,5/5=0,5
=
1-e(-0,4/t)
0,5=e(-0,4/t)
-0,4/t
=ln(0,5)=-0,693
constante de temps:
0,4/0,693=
0,58
microsecondes
0,58
10-6=1000*C
C=0,58
10-9 F
|
|
|
|
|
exercice
4
|
condensateur-champ
électrique-relation courant
tension
|
|
Un
condensateur plan est constitué de
deux armatures métalliques A et B,
surface S=1
dm²,séparées par de
l'air et distantes de 1cm. Il est
chargé tel que QA soit
positive.
e0=1,13
10-11
(répondre
vrai ou faux)
|
- Le vecteur champ électrique
pointe vers A.
- La capacité du condensateur
est 11,3 pF.
- On double la distance des
armatures, la charge restant constante.
Le module du champ électrique
diminue de moitié.
- Relation liant l'intensité
et la tension aux bornes du
condensateur : quelle(s) relation(s)
est(sont) fausse(s)
i=C
dUAB/dt
; i=
dQ/dt
; QB=CUAB.
|
|
corrigé
|
|
faux
le vecteur champ électrique pointe vers le
plus petit potentiel (armature négative)
donc vers B. Entre les
armatures le champ électrique est uniforme.
Le vecteur champ est constant.
vrai
C=1,13
10-11 *0,01 /0,01
C=1,13
10-11 farad =11,3 pF
vrai
la capacité du condensateur est
divisée par deux.
charge =capacité
fois
tension aux bornes ;
la charge étant maintenue constante, la
tension va doubler.
la
tension et la distance
doublent , la valeur
du champ ne change pas.
la
3ème relation est
fausse il faut
écrire
QA=CUAB
|
capacité du
condensateur plan
C
=e0
S / d
farad
....... m²... mètre
e0=1,13
10-11
champ
électrique
E
=
UAB / d
V
m-1 ....... volt...
mètre
|
|
|
|
exercice
5
|
décharge
d'un condensateur et puissance mise en
jeu
|
|
Le flash d'un appareil photo foctionne
gràce à la décharge d'un
condensateur( C=4 mF )chagé sous une tension
de 4,5 V. La décharge complète du
condensateur s'éffectue en 0,1 ms
- Quelle est l'énergie stockée
par le condensateur ?
- Quelle est la puissance mise en jeu au cours
de la décharge ?
- Si la durée da la décharge
double, que devient cette puissance (autres
données inchangées) ?
|
corrigé
|
|
énergie
stockée par le condensateur
=0,5 CU²
0,5*4
10-3*4,5²=
40,5 mJ
la puissance
(watt)est
l'énergie
(joule) divisée
par la durée
(seconde)
P=40,5 10-3 /
10-4 =
405
W
l'énergie
stockée ne change pas mais la durée
double. La
puissance est donc divisée par
2.
|
|
|
cours
|
dipole
RC: équation
différentielle
|
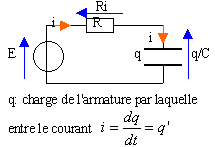
|
équation
différentielle à laquelle
obéit la charge
E=Ri+ q/C
E=Rq'+q/C
q'+ q
/t
= E/R
avec
t=RC
|
|
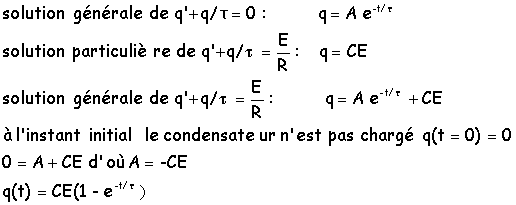
Au bout d'un temps supérieur
à 5 fois la constante de temps , la
charge est constante égale à
q=CE. L'intensité du courant est
nulle i=q'=0
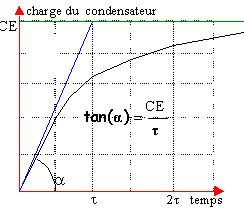
Le coefficient directeur de la tangente
à l'origine est égal
à la valeur de la
dérivée q' (t=0)
Le condensateur aura atteint sa charge
maximale à 1% près au bout
d'un temps t tel que :
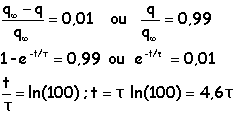
retour
- menu
|
|