Aurélie 06/02
modèles de Thévenin et de Norton

exercices

. .
modèle équivalent de Thévenin :

Un dipole actif linéaire peut être modélisé par une source de tension parfaite associée en série avec une résistance rth.

La fem Eth est égale à la tension u aux bornes du dipôle à vide ( charge débranchée).

La résistance rth du modèle est égale à la résistance équivalente du dipôle actif vue des bornes A et B, en remplaçant tous les générateurs de tension par leur résistance interne, tous les générateurs parfaits de courant par un fil (r = 0), tous les générateurs parfaits de tension par un interrupteur ouvert.

modèle équivalent de Norton :

 Un dipole actif linéaire peut être modélisé par une source de courant parfaite associée en dérivation avec une résistance rth.

La résistance est la même que celle du modèle de Thévenin.

La source de courant parfaite délivre une intensité Icc, égale à celle du courant de court circuit du dipôle actif.

exemple 1 :

  1. Déterminer les élements Eth, rth,et Icc des modèles de Thévenin et de Norton équivalent du dipôle actif linéaire situé à gauche des bornes A et B.
  2. En déduire l'intensité i et les tensions UAB et UDB.

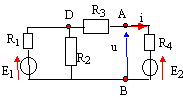
E1 = 40 V ; E2 = 24 V ; R1 = 1W ; R2 = 9 W ; R3 = 2,1 W ; R4 = 2 W.

corrigé

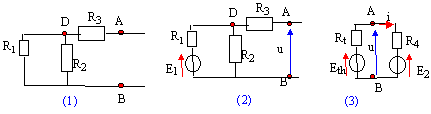
le schéma (1) permet de calculer la résistance équivalente rth :

R1 et R2 en dérivation équivalentes à R = R1R2 / (R1+R2) = 9/10 = 0,9 W.

R et R3 en série équivalentes à rth = R+R3 = 0,9+2,1 = 3 W.

le schéma (2) permet de calculer la fem u = Eth :

aucun courant ne traverse R3 ; soit i l'intensité à travers R1 et R2 :

i = E1 / (R1+R2) et u = R2 i = R2 E1 / (R1+R2) =9*40 / 10= 36 V.

d'où l'intensité Icc du modèle équivalent de Norton : Icc = Eth / rth = 36 /3 = 12 A.

le schéma (3) permet de calculer l'intensité i :

u = Eth - rth i = E2 + R4 i soit i = (Eth - E2 ) / ( rth +R4 ) = (36-24)/ (3+2) = 2,4 A.

uAB = Eth - rth i = 36-3*2,4 = 28,8 V.

uDB = uDA + uAB = R3 i + uAB = 2,1*2,4 +28,8 = 33,84 V.

exemple 2 :

  1. Déterminer les élements Eth, rth,et Icc des modèles de Thévenin et de Norton équivalent du dipôle actif linéaire situé à gauche des bornes A et B.
  2. En déduire l'intensité i et la tension UAB.

I1 = 8 A ; R= 6 W ; E= 4 V; r= 2 W.

corrigé

le schéma (1) permet de calculer la résistance équivalente rth :

R et R en dérivation équivalentes à : rth = RR / (R+R) = 0,5R = 3 W.

le schéma (2) permet de calculer l'intensité de court circuit Icc :

aucun courant ne traverse R , les résistances sont court circuitées par le fil AB

donc I1 = Icc = 8 A et Eth = rth Icc = 3*8 = 24 V.

le schéma (3) permet de calculer l'intensité i :

u = Eth - rth i = E + r i soit i = (Eth - E ) / ( rth + r ) = (24-4)/ (3+2) = 4 A.

uAB = Eth - rth i = 24-3*4 = 12 V.

retour - menu