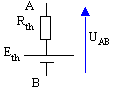. .
Norton, Thévenin électricité sup
exercices de base
cours 1	générateurs équivalents
Calculer les éléments du générateur de tension équivalent au générateur de courant ci contre La capacité vient en série avec un générateur de tension e e= 1/ (jCw) i = 1/(Cw) e-jp/2 e = 1/(Cw) cos(wt-p/2)
cours 2	exemple d'application du th. de thévenin et de Norton
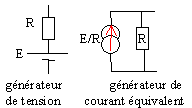
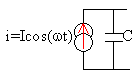
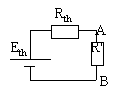
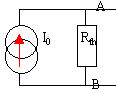
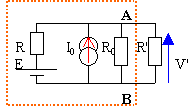
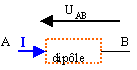
Les théorèmes de Thevenin et de Norton permettent de modéliser des portions de circuit afin de calculer les intensités dans une branche déterminée. Le circuit comprend un générateur de tension continue(E ;R) et un générateur de courant continu(I0 ; R0). Déterminer V'. Quelle intensité traverse R' ? 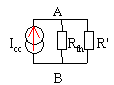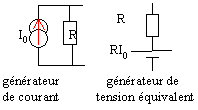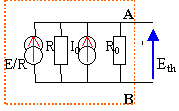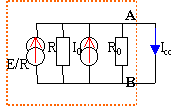modèlisation du dipôle entouré en pointillé rouge transformons (E ; R) en générateur de courant (E/R ; R) Calcul de la résistance équivalente Rth du dipôle vue de A et de B en enlevant toute les forces électromotrices Rth=RR0/(R+R0) résistance du modèle de Thevenin ou de Norton Calcul du courant Icc du modèle de Norton R et R0 parcourues par aucun courant car UAB=0 Icc=I0+E/R et Eth= Icc*Rth modèle thevenin modèle de Norton 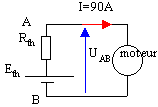calcul de V'=UAB et de l'intensité traversant R'. I = Eth /(Rth+R') et V' =R'I = R'Eth /(Rth+R')
cours 3	rappel : loi d'Ohm généralisée
UAB=SRI-Se E e est nul si le dipôle est un résistor e a le signe de la borne par laquelle on sort d'un dipôle polarisé (pile) e a le sens contraire du courant si le dipôle n'est pas polarisé
exercice 1	batterie déchargée
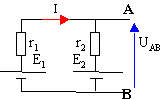
Un automobiliste ne peut plus démarrer sa voiture car sa batterie est partiellement déchargée. On branche en parallèle une deuxième batterie parfaitement chargée. On donne le modèle équivalent de Thèvenin de chaque batterie : .batterie déchargée 10,6V ; 0,03 ohm ;.batterie chargée 12,6V ; 0,02 ohm. Calculer l'intensité du courant circulant dans les batteries. Déterminer le modèle équivalent de Norton de chaque batterie. Déterminer le modèle équivalent de Norton puis de Thèvenin de l'association en parallèle des deux batteries.(On suppose que chaque batterie garde les mêmes caractéristiques après l'association.) On actionne le démarreur. Caluler la tension aux bornes de l'ensemble si le démarreur absorbe 90 A. Quelle serait l'intensité du courant circulant dans les deux batteries si, par erreur, on reliait les bornes + avec les bornes - ? corrigé r1I - E1 + r2I +E2 = 0 I= (E1 - E2 ) / ( r1 + r2) = 40 A par contre si on relie la borne + de la batterie 1 à la borne - de l'autre on trouve I= (E1+ E2 ) / ( r1 + r2) = 434 A résistance du modéle de Thevenin ou de Norton : en supprimant les deux fem il reste 2 résistances en dérivation Rth=r1r2/(r1+r2)= 0,012 W. Calcul de Eth : Eth = UAB= r2I + E2 I= (E1 - E2 ) / ( r1 + r2) Eth = (E1r2 + E2r1 ) / ( r1 + r2) = 11,8 V donc l'intensité I0 du modéle de Norton est Eth/Rth = 983,3 A UAB= Eth - Rth I= 10,72 V modéle de Thevenin modéle de Norton
exercice2	Thévenin en courant alternatif
On néglige la résistance de la self, L=10 mH. R=390 W , i=10-3 cos(wt); C=20 nF ; f=16kHz. Dans ces conditions i et V' sont en opposition de phase et V'=-Ri. 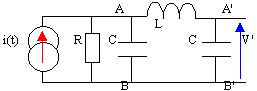donner le générateur de Thévenin vu des bornes A' et B' par une charge Z1. corrigé Soit Y l'admittance complexe du circuit constitué par R et C en parallèle. Y=1/R+jCw. Eth=V'=-Ri 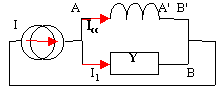Calcul du courant de court circuit Icc si A' et B' sont réunis. (fig ci dessus) toutes les grandeurs sont complexes. I = I1 + Icc et Icc jLw= I1/ Y d'où Icc= I/(1+ jYLw) Icc=I/(1+(1/R+jCw)jLw)) = I/(1-LCw²+ jLw/R) dans ce cas LCw²=2 donc Icc = I/( jLw/R-1) Impédance Zth du générateur de Thévenin. Zth=Eth/Icc = -R( jLw/R-1) = R- jLw =R+ 1/(jC/2w) Les éléments du générateur de Thévenin sont: Eth=-Ri et d'impédance interne R en série avec un condensateur de capacité C/2.
exercice 3	Thévenin en courant alternatif
Déterminer les éléments du générateur de Thévenin équivalent vu par Z entre A et B. On pose x=RCw. e générateur parfait
corrigé
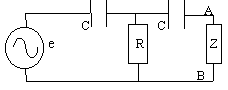
fem du générateur de Thévenin V en grandeurs complexes V= RI et I = e /(R+1/jCw) V= eR/(R+1/jCw)=ejRCw/(1+jRCw) V=ejx/(1+jx)
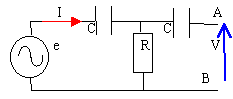
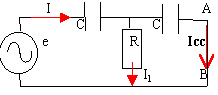
impédance du générateur de Thévenin admittance Y de R et C en dérivation en grandeurs complexes Y=1/R+jCw 1/Y=R/(1+jx) Zth=R/(1+jx) + 1/jCw. Zth=1/jCw(1+2jx)/(1+jx)		Icc=Eth/Zth=ej²Cw/(1+2jx) courant du modèle de Norton
retour - menu