cinématique quelques exercices plus difficiles
		. .
exercice 1	dépassement - mouvement uniforme
Un automobile de longeur l=5 m, roulant à la vitesse Va=90 Km.h-1 arrive derrière un camion de longeur L=10m, roulant à une vitesse Vc=72 Km.h-1. Les deux véhicules conservent des vitesses constantes. L'automobile va donc doubler le camion. en admettant que le dépassement commence quand l'avant de l'automobile est à la disance d1=20m de l'arrière du camion et se termine quand l'arrière de l'automobile est à la distance d2=30m de l'avant du camion. Calculer La durée du dépassement . La distance parcourue sur la route par la voiture pendant le dépassement. corrigé exprimer les vitesses en ms-1 en divisant par 3,6 Va=90/3,6 = 25 ms-1 ; Vc=72/3,6=20 ms-1. distance parcourue par la voiture en t seconde 25t = 20 + 10 + 20 t + 30 + 5 t = 13 s et la voiture parcourt 25*13= 325 m
exercice 2	mouvement sur un axe
On étudie le mouvement d'un mobile ponctuel sur un axe (O ; i). Ses caractéristiques sont: accélération constante : 4 ms-²; abscisse initiale: 1 m; vitesse initiale : -3 ms-1. Quelle est la nature de ce mouvement? Ecrire l'équation de la vitesse Vx(t) et l'équation horaire x (t) Déterminer les dates auxquelles le mobile passe à l'origine 0. Quelle est alors la vitesse? Que peut-on déduire sur le mouvement du mobile? Au cours de son évolution, le mobile change-t-il de sens de parcours? Si oui, donner la date et la position correspondant à ce changement? corrigé mouvement rectiigne uniformément freiné , arrêt, puis accélération. vitesse,: primitive de l'accélération : v(t)=4t-3 abscisse, primitive de la vitesse : x(t)= 2t²-3t+1 passage à l'origine : 0=2t²-3t+1 solutions : t=0,5 et t=1 s 0 à 0,75 s: le mobile se déplace en sens contraire de l'axe, passe à l'origine à la date 0,5 s. 0,75 s : arrêt puis déplacement dans le sens de l'axe et nouveau passage à l'origine à t=1 s. arrêt si v=0 soit t= 0,75 s position: 2*0,75²-3*0,75+1= -0,125 m
exercice 3	voyageur en retard
Un voyageur en retard court le long du quai à la vitesse constante V= 6 m.s-1. Quand il est à 20m du dernier wagon du train qui démarre avec une accélération constante a= +1 m.s-2 ( le train et le voyageur ont des trajectoires rectilignes parallèles.) Définir le repère dans lequel le mouvement est étudié. Préciser su le schéma les positions, les dates et les vitesses connues. Ecrire dans un même repère les équations horaires du voyageur et du dernier wagon considérés comme des points matériels. Montrer que le voyager ne peut pas rattraper le train . Quelle sera la distance minimale entre le voyageur et le dernier wagon? corrigé pour t=0 lorsque le train démarre.; X0=0 position du dernier wagon abscisse voyageur x1=6t-20 abscisse dernier wagon x2=0,5.a.t²=0,5 t² si le voyageur ratrappe le train x1=x2 ; 0,5 t²-6t+20=0 D=36-40, est négatif donc il n'y a pas de solution à notre équation ; le voyageur ne rattrapera jamais le train. Distance entre le dernier wagon et le voyageur : x2-x1 =0,5 t²-6t+20 Cette distance est minimale lorsque la dérivée par rapport au temps de cette fonction s'annule. t-6=0 ; t = 6 secondes x2-x1 = 0,5*6²-6*6+20 = 2 m
exercice 4 La voiture et le piéton Une voiture de largeur L=1,4 m se déplace à vitesse constante v=72 km h-1 en suivant le bord de la route de largeur 2L. Un piéton est à la distance d=50 m devant la voiture , au bord de la route. Il veut traverser à vitesse constante notée u. (a=45°) Quelle est la valeur minimale de u afin que le piéton ne soit pas touché. Pour quelle valeur de a, la vitesse minimale du piéton est-elle minimale ? Quelle est sa valeur ? 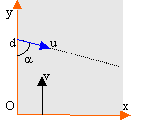corrigé coordonées des vecteurs vitesses dans le repère ci dessus : piéton : u sin a ; - u cos a voiture : 0 ; v coordonées des vecteurs positions dans le repère ci dessus : piéton :x= u sin a t ; y= - u cos a t +d voiture :x= 0 ; y= v t Le piéton n'est pas écrasé s'il atteint l'abscisse x=L avant que la voiture ne le touche. soit t= L / (u sin a) positions à la date t : piéton : yP= - u cos a L / (u sin a) +d= - cotan a L +d voiture : yV= v L / (u sin a) yP> yV soit : - cotan a L +d > v L / (u sin a) u > 72/3,6 *2,8 / (-1,4*cos(45)+50sin(45)) u > 0,814 ms-1 ou 2,93 km h-1. La vitesse u sera la plus faible lorsque le dénominateur -Lcos a + d sin a sera le plus grand possible. On dérive par rapport à a l'expression -Lcos a + d sin a et on recherche la valeur de a qui annule cette dérivée. L sin a + d cos a = 0 ou tan a = -d/L = -50/1,4 = -35,71 a = 91,6 °
exercice 5	cinématique terminale
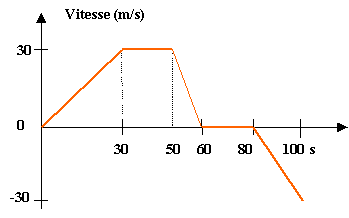
I Sur un axe, un point mobile M est repéré par son abscisse x = - 4t2+ 6,4t Quelles sont les coordonnées du vecteur vitesse, du vecteur accélération ? Quelle est la vitesse initiale ? Déterminer les intervalles de temps durant lesquels le mouvement est accéléré ou retardé. Déterminer la position du point de rebroussement. II - Un véhicule se déplace sur un trajet rectiligne. Sa vitesse est caractérisée par le diagramme ci dessus. Indiquer sur les 5 intervalles de temps : la valeur algébrique de l'accélération a. l'expression V= f(t) on utilisera au début de chaque phase un nouveau repère de temps. la nature du mouvement. corrigé vitesse : dérivée de l'abscisse par rapport au temps v = - 8t+ 6,4 accélération : dérivée de la vitesse par rapport au temps a = - 8 vitesse initiale : 6,4 m/s. La vitesse s'annule à t = 0,8 s position d'arrêt. sur[0 ; 0,8 s] mouvement rectiligne uniformément freiné au delà de 0,8 s , après avoir rebroussé chemin, le mobile accélère. [0 ; 30 s] [30 ; 50 s] [50 ; 60 s] [60 ; 80 s] [80 ; 100 s] accélération : coef directeur de la droite 1 0 -3 0 -1,5 vitesse: primitive de l'accélération 1t 30 -3 t+30 0 -1,5 t mouvement accéléré uniforme freiné arrêt retour - menu - menu accéléré au début de chaque phase t = 0.
exercice 6	freinage sur autoroute
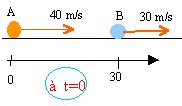
Sur une autoroute 2 voitures roulent sur la même file avec une vitesse de 40m/s. Le pare chocs avant A de la seconde voiture est à 40m derriere le pare chocs arriere B de la premiere voiture. Le véhicule B freine avec une décélération de 5 m/s² . Le véhicule A distrait freine 2s après avec la même décélération. Quelle distance parcourt le deuxieme véhicule avant de commencer à freiner ? Quelle distance parcourt le premier véhicule pendant ce même temps ? Quelle est la distance séparant A et B lorsque le second véhicule commence à freiner ? Quelle est la vitesse du premier véhicule à ce moment ? En prenant comme origine des dates l'instant où débute le freinage du second véhicule et comme origine des espaces la position où il se trouve alors, établir les équations horaires des mouvements de A et B. Un choc aura t il lieu? Si oui à quelle date? corrigé on doit multiplier 40 m/s par une durée en seconde distance parcourue par le 2ème véhicule d'un mouvement uniforme : 40*2 = 80 m. distance parcourue par le 1er véhicule d'un mouvement uniformément retardé d= ½ a t² + 40 t = -2,5 *4 + 40*2 = 70 m . distance entre les véhicules : 40 - différence des deux résultats précédents : 40-10 = 30 m. vitesse du premier véhicule à t=2 s : v = at + 40 avec a négatif : -5*2+40 = 30 m/s à t=0 1er véhicule situé 30 m devant l'autre; vitesse initiale 30 m/s ; a =-5 m/s² x1 = -2,5 t² +30 t +30 second véhicule : à t=0 ; vitesse initiale 40 m/s; accélération = -5 m/s² x2 = -2,5 t² + 40t choc si x1= x2 -2,5 t² +30 t +30 = -2,5 t² +40t 30t +30 = 40 t à t=3 s.
exercice 7 Dans le repère Oxy les équations horaires des coordonnées du point mobile M sont données par : x = A. cos(wt) y = A. sin(wt) Donner les expressions des vecteurs vitesse et accélération .Montrer que le vecteur accélération est colinéaire au vecteur OM. Quelle est l'équation de la trajectoire de M dans le repère cartésien ? Quelle est la nature de cette trajectoire? Donner également l'équation horaire de l'abcisse curviligne du point M en prenant comme origine Mo , position du mobile à l'insant t = 0. corrigé dérivée de sin (w t) donne w cos (wt ) dérivée de cos (wt ) donne -w sin (wt ) le vecteur vitesse est la dérivée du vecteur position OM. Vx = -Aw sin (wt ) Vy = Aw cos (wt ) le vecteur accélération est la dérivée du vecteur vitesse : ax = -Aw² cos (wt) = -w² x ay = -Aw² sin (wt) = -w² y trajectoire : penser à sin² (wt) + cos² (wt )= 1 x² + y² = A²cos² (wt ) +A²sin² (wt) = A² cercle de centre O, de rayon A Mo( A ; 0) en remplaçant t par 0 dans x et dans y. abscisse curviligne :MoM ( x-A ; y) MoM²= (x-A)² + y² : remplacer x par A cos (wt ) et y par A sin (wt ) A²(cos(wt ) -1)² + A²sin² (wt )= A²[ cos² (wt )-2 cos(wt )+1 +sin² (wt )] MoM²= 2A² (1-cos(wt )) = 4A² sin² (½(wt )) MoM =2A sin (½(wt )).
retour - menu - menu