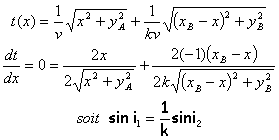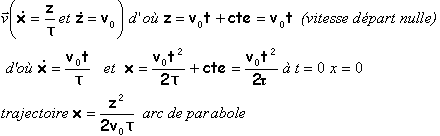cinematique

cinématique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

le sauveteur

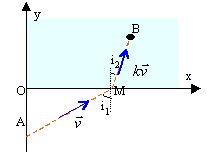Un touriste (A) se promène au bord d'un lac ; il aperçoit une personne qui se noie (B). Pour venir à son aide il court sur la rive à la vitesse v constante et nage à la vitesse kv constante (k< 1).

Déterminer la relation liant les angles i₁ et i₂ afin que la durée du trajet soit minimale. L'abscisse de M est notée x.

corrigé

durée du déplacement AM:

durée du déplacement MB dans l'eau:

La position de M correspondant à la durée minimale est obtenue en dérivant le temps par rapport à x et en recherchant la valeur de x qui rend cette dérivée nulle.

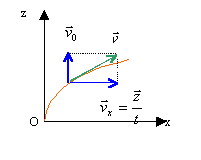
ballon sonde : lois horaires

Un ballon sonde a une vitesse verticale v₀ indépendante de l'altitude. Le vent lui communique une vitesse hotizontale proportionnelle à l'altitude atteinte.

Déterminer les lois horaires du mouvement et déterminer l'équation de la trajectoire.

corrigé

vecteur vitesse tangent à la trajectoire

ballon sonde : accélération

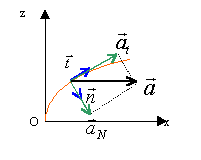
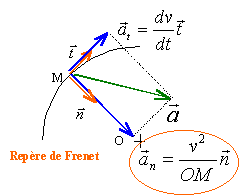
Déterminer l'accélération. Comment évolue le rayon de courbure ?

corrigé

Composantes de l'accélération : dériver par rapport au temps les composantes du vecteur vitesse

Composantes de l'accélération dans le repère de Frenet :

le rayon de courbure de l'arc de parabole croît avec le temps.

vitesse, accélération, repère de Frenet :

On donne les équations paramètriques de la trajectoire plane d'un point mobile par rapport à un référentiel : x= 2t et y= 4t²-4t

Déterminer l'équation de la trajectoire.
Calculer la vitesse du mobile.
Montrer que son accélération est constante.
Déterminer les composantes normale et tangentielle de l'accélération dans un repère de Frenet.
En déduire le rayon de courbure.

corrigé

éliminer le temps entre x et y : t= ½x ; report dans y

y= x²-2x trajectoire parabolique.

vecteur vitesse : dérivée par rapport au temps du vecteur position v (dx/dt = 2 ; dy/dt = 8t-4)

valeur (norme) de la vitesse : v² = v_x²+v_y² =4+(8t-4)² = 64t²-64t-20 en m s^-1.

vecteur accélération : dérivée par rapport au temps du vecteur vitesse a (dv_x/dt = 0 ; dv_y/dt = 8)

valeur (norme) de l'accélération : a² = a_x²+a_y² =0+8² soit a = 8 m s^-2, indépendante du temps.

vecteur accélération tangentielle, colinéaire au vecteur vitesse :

a_T=dv/dt avec v = [4+(8t-4)²]^½.

a_T= dv/dt = 16(8 t -4)*½* [4+(8t-4)²]^-½=8(8 t -4) [4+(8t-4)²]^-½.

a² = a²_T+ a²_N soit a²_N = a²-a²_T= 8² -8²(8 t -4)² [4+(8t-4)²]^-1.

réduire au même dénominateur [4+(8t-4)²] :

a²_N =8²*4 [4+(8t-4)²]^-1 soit a_N= 16[4+(8t-4)²]^-½.

le rayon de courbure r est liée à l'accélération normale a_Net à la vitesse v : a_N= v²/r .

r = v² / a_N= [4+(8t-4)²]^-3/2/16.

trajectoire circulaire

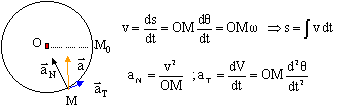Le plan est rapporté à un repère ortonormé xOy d'origine O et de base (i, j). Les coordonnées s et y d'un point M mobile dans le plan (O,i, j) varient avec le temps suivant : x= 2 cos (5t) et y= 2 sin (0,5 t).

Déterminer la nature de la trajectoire.
Déterminer les composantes du vecteur vitesse v.
Déterminer l'expression de la vitesse ds/dt ainsi que de l'abscisse curviligne s du point M à l'instant t, en prenant comme condition initiale s=0 quand t=0
Déterminer les composantes normale et tangentielle de l'accélération dans un repère de Frenet.
En déduire le rayon de courbure de la trajectoire.
La trajectoire reste la même, mais maintenant le point M subit une accélération angulaire d²q/dt²=q" = 0,2 t. A quelle date le point M atteint-il une vitesse de 10 m/s , sachant qu'il est parti du repos. Quelle distance a-t-il alors parcouru ?

corrigé

la trajectoire s'obtient en éliminant le temps entre les deux équations paramètriques :

x²+y² = 4cos² (5t) + 4sin² (0,5 t) = 4, cercle de centre O et de rayon R=2.

les composantes du vecteur vitesse sobtiennent en dérivant x et y par rapport au temps :

v_x= 2*0,5 (-sin(0,5t)) = - sin (0,5t) ; v_y= 2*0,5 cos(0,5t) = cos (0,5t)

valeur numérique de la vitesse v² = v²_x+v²_y= sin²(0,5t) + cos²(0,5t) ; v = 1 m/s.

abscisse curviligne s : intégrer v : s= t + cte

or à t=0 , s=0 d'où s=t.

les composantes du vecteur accélération sobtiennent en dérivant v_x et v_y par rapport au temps :

a_x= -0,5 cos(0,5t); a_y= -0,5 sin(0,5t)

a² = a²_x+a²_y= 0,25 cos²(0,5t) + 0,25 sin²(0,5t) =0,25 m/s².

Dans la base de Frenet : acélération tangentielle a_T= dv/dt =0 ( car v=1 = constante);

acélération normale : a² = a²_N+a²_T d'où a = a_N car a_T=0 ; a_N= 0,5 m/s² .

rayon de courbure ( rayon du cercle dans un moucement circulaire) : a_N= v²/R soit R= v²/a_N=1²/0,5 = 2 m.

accélération angulaire q"= dw/dt = 0,2 t

par intégration on obtient la vitesse angulaire w (rad/s) : w = 0,1 t²+ cte , le mobile étant parti du repos la constante d'intégration est nulle et : w = 0,1 t².

La vitesse linéaire est v= w R = 0,1R t² = 0,1*2 t² = 0,2 t².

la valeur 10 m/s est atteinte à la date t telle que :10 = 0,2 t² soit t = 7,1 s.

distance parcourue à cette date : par intégration de la vitesse angulaire on détermine l'angle q dont M à tourner

q =0,1 /3 t³ puis s = Rq = 0,1/3*2 t³ = 1/15 *7,1³= 23,86 m.

position du point M à cette date : q = s/R= 23,86/2 = 11,8 rad soit 11,8 *180/3,14 = 676 °

676°=360°+316° (voir figure ci-dessus)

composantes de l'accélération aà cette date : a_N= v²/R= 10²/2= 50 m/s² ;

a_T= Rq"= 2*0,2t = 0,4*7,1 = 2,84 m/s².

traversée de la rivière

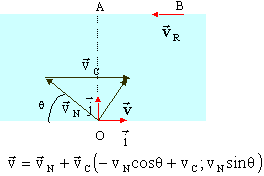Un sportif se propose de traverser une rivière de largeur d =50 m en plongeant à partir du point O de la rive. la vitesse du courant v_C est supposée constante de valeur 1 m/s. Il s'agit d'arriver le plus vite possible en face du point de départ. Pour cela il devra nager , puis courir sur la rive opposée. La vitesse du nageur par rapport à l'eau est v_N= 1,2 m/s. Sa vitesse de course par rapport à la rive est v_R=21,6 km/h. La norme et la direction des vecteurs vitesses restent constantes.

Quelle orientation le nageur doit-il conserver par rapport à la rive ?
Calculer la distance AB parcourue sur la rive opposée ainsi que le temps total mis par le sportif pour atteindre son but.

corrigé

On exprime la durée totale du trajet ; puis on la minimise.

Le trajet comporte la partie OB parcourue à la vitesse absolue v, et la partie BA parcourue à la vitesse v_R.

La vitesse utile du nageur est la projection de v_N sur j. L durée du parcours OA est t₁ = d / (v_Nsinq)

durée du parcours BA : t₂ = AB/v_R ; durée totale t =d / (v_Nsinq) +AB/v_R ;

or AB =( v_C-v_Ncosq)t₁=( v_C-v_Ncosq)d / (v_Nsinq)

t =d / (v_Nsinq)[1+ ( v_C-v_Ncosq) /v_R].

dériver t par rapport à q : la durée sera minimale si cette dérivée est nulle.

u = d / (v_Nsinq) ; u'= -d cosq /(v_Nsin²q)

w =1+ ( v_C-v_Ncosq) /v_R; w' = v_Nsinq /v_R;

( dérivée d'un produit) u' w + w' u =d[v_N-(v_R+v_C)cosq] / (v_R v_N sin²q)

cette expression s'annule pour v_N-(v_R+v_C)cosq=0 soit cosq = v_N/(v_R+v_C).

application numérique : v_R=21,6 / 3,6 =6 m/s ; cos q =1,2 / (6+1)=0,171 soit q =80,1°.

distance AB =( v_C-v_Ncosq)d / (v_Ncosq)

AB=(1-1,2*0,171)*50 / (1,2*sin 80)]=39,74 /1,182 =33,6 m.

durée totale du parcours : t =d / (v_Nsinq) +AB/v_R= 50 / (1,2 sin80) +33,6 / 6 = 42,3 + 5,6 = 47,9 s.

Dans le plan xOy, une droite Ox' rourne autour de l'axe Oz avec une vitesse angulaire w = dq/dt = constante. Un mobile m (OM=r) se déplace sur la droite Ox' d'un mouvement rectiligne uniformément accéléré d'accélération a. A l'instant initial M se trouve en M₀, au repos, puis s'éloigne de O.

Déterminer les expressions littérales vectorielles des vitesses relative, d'entraînement et absolue de M
Déterminer les expressions littérales donnant la norme et la direction du vecteur vitesse absolue du point M.
Si l'axe Ox' est confondu avec l'axe Ox à l'instant initial, calculer les coordonnées du point M à la date t=3 s. Dessiner les 3 vecteurs vitesses à cette date.
Déterminer les expressions littérales vectorielles dans une base polaire des accélérations relative, d'entraînement et de Coriolis de M.
Déterminer les expressions littérales donnant la norme et la direction du vecteur accélération absolue du point M..
Dessiner ces vacteurs accélérations à t =3s.
données : OM₀= 1 cm ; a = 2 cm/s²; w =p/5 rad/s.

corrigé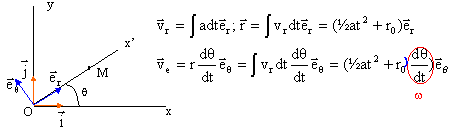

la vitesse relative est la vitesse de M par rapport à la tige Ox' ; la vitesse est une primitive de l'accélération ; la position est une primitive de la vitesse.

la vitesse d'entraînement est celle du point coïncodent : c'est celle du point M solidaire de la tige Ox', en rotation autour de Oz.

La vitesse absolue est la somme vectorielle de ces deux vitesses.

norme de la vitesse absolue : v_a²= v_r² + v_e² = (at)² + ((½at²+r₀)w)²

direction du vecteur vitesse absolue : a = angle entre la tige Ox' et le vecteur vitesse absolue :

tan a = v_q/v_r=((½at²+r₀)w) / (at)

application numérique : t= 3s ; r₀= 0,01 m ; a= 0,02 m/s²;

q = w t = 3,14/5*3 = 1,884 rad soit 1,884*180/3,14 = 108°.

r = ½at²+r₀ = 0,5*0,02*9+0,01 = 0,1 m ; x = 0,1 cos 108 = -0,031 m ; y= 0,1 sin108 =0,095 m;

v_r= at = 0,02*3 = 0,06 m/s ; v_e=(½at²+r₀)w) = (0,5*0,02*9+0,01)*3,14/5= 0,0628 m/s.

v_a = (0,06²+ 0,0628²)^½=0,087 m/s.

l'accélération absolue est la somme vectorielle des trois accélérations relative, de Coriolis et d'entraînement.

a_a = a_r+ a_c+ a_e=(a-w²r)e_r + 2atwe_q avec r = ½at²+r₀.

norme de l'accélération absolue a_a=[(a-w²r)² +(2atw)²]^½.

direction de l'accélération absolue : soit b l'angle entre la tige et le vecteur accélération absolue

tan b = 2atw /(a-w²r)

application numérique : r = 0,1 m ; t= 3s ; r₀= 0,01 m ; a= 0,02 m/s²; w =3,14/5 = 0,628 rad/s

a-w²r = 0,02-0,628²*0,1 = -0,0194 m/s² ; 2atw =2*0,02*3*0,628 =0,0754 m/s²

a_c= w²r = 0,628²*0,1 = 0,0395 m/s².

a_a=[(-0,0194)²+0,0754²)]^½=0,078 m/s².

tan b =0,0754 /(-0,0194) = -3,886 ; b = -75°.

retour - menu