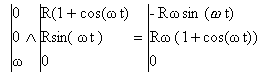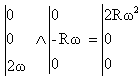Aurélie 02 /02
changement de référentiels

le mouvement d'entraînement est une translation

le mouvement d'entraînement est une rotation

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts
. .
.
.

Un disque de rayon r tourne uniformément autour de son axe, à vitesse angulaire w, dans le sens indiqué sur la figure. Son centre C se déplace sur la droite horizontale z = r du plan vertical Ozx du référentiel R=Oxyz. On appelle R' le référentiel Cxyz, en translation par rapport à R, d'origine C, et on note q l'angle que fait un rayon CA du disque avec Cz. A étant un point de la péripherie.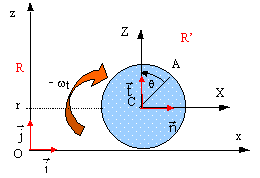

  1. Exprimer, dans la base de R, la vitesse et l'accélération de A par rapport à R'.
  2. Quelle vitesse, par rapport à R, doit on donner à C pour que la vitesse VB/R(vitesse de B dans R) du point le plus bas B du disque soit nulle ?
  3. Trouver les équations x =x(q) et z=z(q) du point A, sachant que pour q =0, x=0 et z =2r.

 

corrigé
on étudie le point A :

les vecteurs sont écrits en bleu et en gras.

relation entre les vecteurs vitesses :

OA = OC + CA

dOA /dt = dOC /dt + dCA /dt

vecteur vitesse de A dans R = vecteur vitesse de C dans R + vecteur vitesse de A dans R'

VA/R = VC/R + VA/R'

dans le référentiel R' le disque roule sans glisser : q = w t avec w = q ' = cte.

on note X l'abscisse et Z l'ordonnée de A

X = r sin(w t) et Z= r cos (w t) ( à t= 0 X= 0 et Z= r)

vitesse de A dans R' : dériver X et Z par rapport au temps

X' = r w cos (w t) n et Z' = -r w sin (w t) t.

dans le référentiel R on note x l'abscisse et z l'ordonnée de A

translation suivant z C= r ; on suppose la vitesse de translation constante notée v suivant l'horizontale xC = v t

vitesse de C dans R : dériver xC et z C par rapport au temps

x'C = v i et z'C = 0 j.

d'où la vitesse de A dans R :

x'A = (r w cos (w t) + v)i ; z'A = - r w sin q j.

accélération dans R : dériver à nouveau par rapport au temps

x" = - r w ² sin (w t) i et z" = -r w ² cos (w t) j .

le vecteur accélération est centripète, dirigé vers C

au point le plus bas : q = p

x'( wt = p ) = -r w + v et z ' (wt = p) = 0

la vitesse en B est nulle si v = r w.

 

Dans un plan Oxy un cercle de diamètre OA tourne à la vitesse angulaire constante w autour du point O. On associe au centre du disque deux axes rectangulaires CX et CY. A t= 0 le point A est sur Ox et un point M initialement en A parcourt la circonférence dans le sens contraire au sens trigonométrique avec la vitesse angulaire w.

  1. Exprimer les composantes des vecteurs vitesse et accélération de M dans le repère Oxy.
  2. Exprimer les composantes des vecteurs vitesse et accélération de M dans le repère CXY.
  3. Déterminer les expressions de la vitesse d'entraînement et l'accélération complémentaire.

 

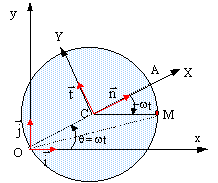
corrigé
dans le repère Oxy :

q = w t ; l'abscise de M est notée x, l'ordonnée est noté y.

OM = OC + CM.

repère Oxy : OC [xC = R cos (w t) ; yC =R sin (w t) ] et CM ( R ; 0 )

OM [ x =R(1+cos (w t) ; y =R sin (w t) ]

vitesse de M : dériver x et y par rapport au temps.

VM/ Oxy [-Rw sin (w t) ; Rw cos (w t) ]

accélération de M : dériver le vecteur vitesse par rapport au temps.

gM/ Oxy [-Rw² cos (w t) ; -Rw² sin (w t) ]

dans le repère C XY :

q = -w t ; l'abscise de M est notée X, l'ordonnée est noté Y.

CM [ X = Rcos (w t) ; Y= -R sin (w t) ]

vitesse de M : dériver X et Y par rapport au temps.

VM/ C XY [-Rw sin (w t) ; -Rw cos (w t) ]

accélération de M : dériver le vecteur vitesse par rapport au temps.

gM/ C XY [-Rw² cos (w t) ; Rw² sin (w t) ]

vitesse d'entraînement
vitesse absolue par rapport à O xy ( R)
vitesse relative par rapport à C XY ( référentiel R')
vitesse d'entrainement Ve
V M / R
= V M / R'
w R'/R^ OM
calcul de : w R'/R^ OM

accélération d'entraînement :

la rotation étant uniforme dw /dt =0

l'accélération d'entraînement est : ge = -w ² OM.

ge [ w ²R(1 +cos(w t) ; -w ²R sin(wt) ; 0]

accélération complémentaire : gc = 2 w ^ VM/ R' =2 w ^ (VM/ R - Ve )

 

 

retour - menu