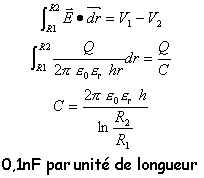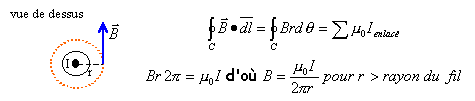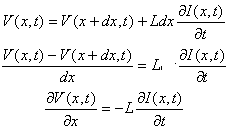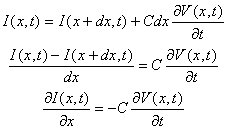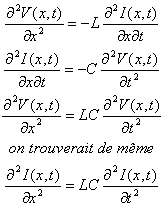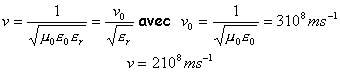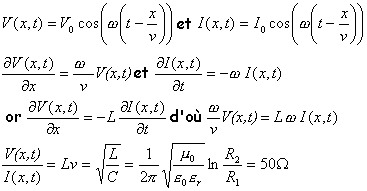notions de base

(quiz)

ondes sonores

ondes sur une corde

Ondes électromagnétiques se propageant dans un câble coaxial d'après Capes 94

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


 

1

capacité linéique du cable coaxial
Un câble coaxial comprend deux cylindres conducteurs, l'un creux de rayon R2, l'aute plein de rayon R1; ils ont le même axe ; un isolant de permitivité er les sépare.
  1. Définir la capacité d'un condensateur
  2. Donner les caractéristiques du champ électrique en un point M de l'isolant
  3. Déterminer la capacité du condensateur constitué par une longueur h du câble. Quelle est la capacité linéique du câble .R1=0,5 mm; R2=1,75 mm ;er=2,25
    corrigé


La capacité C (farad (F)) d'un condensateur dont l'armature au potentiel V1 porte la charge Q (coulomb) (l'autre armature au potentiel V2 porte la charge -Q) est définie par :

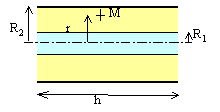
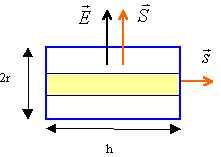
Q = C(V1-V2).

Le champ électrique est radial. On applique le théorème de Gauss à un cylindre de rayon r compris entre R1 et R2 et de hauteur h.

Le flux à travers les bases du cylindre est nul ( vecteurs champ et surface perpendiculaires). Sur la surface latérale on écrit :

2prh E = Q /(e0er) ou E = Q /(2prhe0er)

Puis exprimer la circulation du champ le long d'un rayon :

 
2

auto-inductance linéique du câble
 

 

Les courants et les tensions qui se propagent dans le câble sont de fréquences élevées.Quel phénomène accompagne le passage du courant dans un métal très bon conducteur ?

  1. Quelle est l'expression du champ magnétique crée par un fil , parcouru par un courant I, en un point situé au voisinage de ce fil ?
  2. On peut considérer que des courants I circulent en sens inverse sur les cylindres de rayons R1 et R2 . En utilisant le théorème d'Ampère, déterminer en un point M de l'isolant le champ magnétique ? Que vaut-il hors isolant ?
  3. Définir inductance propre d'un circuit.
  4. Calculer le flux du champ magnétique à travers le contour EFGH et en déduire le coefficient d'auto-inductance linéique du câble. Le calculer avec les données précédentes.
corrigé


 

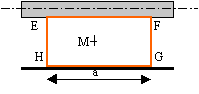
Le métal étant bon conducteur, les courants sont surfaciques; ce phénomène s'appelle effet de peau.

Le champ magnétique est orthoradial, il ne dépend que de r. Le sens du champ est obtenu à partir de la règle du bonhomme d'Ampère. L'expression du champ se détermine à partir du théorème d'Ampère. (circulation du champ sur un contour circulaire)

Dans le cas du câble le résultat précédent s'applique pour R2>r>R1.

si r >R2, la somme des courants enlacés est nulle (I dans le conducteur central et -I dans le conducteur extérieur). Le champ magnétique est nul à l'extérieur du câble.

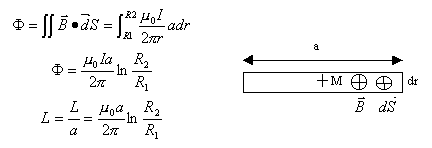
L'inductance L (henry (H) ) est définie par la relation F = LI

F est le flux propre

application numérique : L= 0,25 mH par mêtre de câble.

3

équation d'onde dans le câble
 

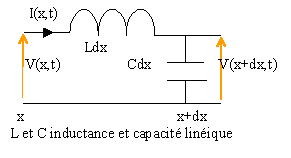
Un élément du câble coaxial de longueur dx peut être représenté par le schéma ci dessus.

  1. En appliquant les lois de l'électricité à ce modèle trouver les deux équations aux dérivés partielles liant intensité et tension.
  2. En déduire les équations d'onde vérifiées pat V(x,t) et I(x,t).
  3. Exprimer la vitesse de propagation de ces ondes puis la calculer.
    corrigé


loi des mailles :

loi des noeuds :

Puis on dérive les équations précédentes respectivement par rapport à x et à t.

On pose 1 / v² = LC puis on remplace L et C par les expressions trouvées précédemment :
4

résistance de la ligne
 

 

Soit V(x,t) une onde de tension sinusoïdale, progressive, de fréquence N se propageant le long du câble supposé très long. Ecrire les tensions V(x,t) et I(x,t) et en déduire la résistance de la ligne. Calculer cette résistance.

corrigé


 

5

ligne coaxiale fermée sur une résistance
Le câble de longueur L est alimenté à l'une de ses extrémités par un générateur délivrant une tension de pulsation w et fermé à l'extrémité d'abscisse L par une résistance R. Dans ces conditions l'onde émise par le générateur va se réfléchir au bout de la ligne. En un point M, l'onde résultante est la superposition de l'onde incidente et de l'onde réfléchie.
  1. Ecrire les relations liant V0(x,t), I0(x,t) d'une part et V1(x,t), I1(x,t) d'autre part. (V0 et V1 ondes de tension incidente et réfléchie)
  2. Exprimer le coefficient de réflexion I1 / I0 en fonction des résistances.
  3. Proposer une méthode permettant de mesurer la vitesse de propagation des ondes le long du câble ainsi que la valeur de Rligne.
    corrigé


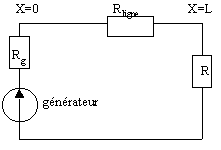
loi des noeuds en un point M de la ligne : I(M,t)=I0(x,t)-I1(x,t)

loi d'Ohm pour la tension incidente : V0(x,t)=Rligne I0(x,t)

pour la tension réfléchie : V1(x,t)=Rligne I1(x,t)

En bout de ligne : V(L,t)=R I(L,t) = V0(L,t)+V1(L,t)

--> R I(L,t) = RligneI0(L,t) + Rligne I1(L,t)

En bout de ligne : I(L,t)=I0(L,t)-I1(L,t)

--> R(I0(L,t)-I1(L,t)) = Rligne(I0(L,t) + I1(L,t))

(Rligne-R) I0(L,t) = -(Rligne+R) I1(L,t)

I1(L,t) / I0(L,t) = (R-Rligne) / (Rligne+R)

Pour mesurer la vitesse de propagation, prendre un osciloscope à mémoire, un GBF, et un câble de longueur L. Fermer le câble sur une impédance nulle (court circuit). L'impulsion réfléchie est enregistrée avec un retard 2L/v; on peut en déduire v.

Pour mesurer Rligne, on place un potentiomètre de résistance RP au bout du câble; lorsque RP = Rligne la réflexion est nulle.

retour - menu