d'après concours Kiné Rennes 2000 exercice suivant : chimie chute d'une boule le long du mât d'un navire
1	divers circuits RL ; RLC
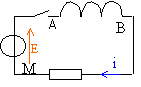
On veut connaître les caractéristiques électriques L (inductance) et r (résistance) d'une bobine d'allumage B. On branche cette bobine en série avec un interrupteur K aux bornes d'un générateur idéal de tension continue E=6V. Établir l'équation différentielle (écrire les lois d'Ohm pour chaque dipole) donnant l'intensité du courant i(t) dans le circuit lorsque l'on ferme l'interrupteur. Sachant que la solution de cette équation différentielle est donnée par i(t) =A(1-exp-t/t), donner les expressions littérales de la constante de temps t en fonction de L et r et de la constante A en fonction de E et R. Un oscilloscope est branché entre les points A et M du circuit > - Avant fermeture de l'interrupteur, quel graphe observe-t-on ? - Après fermeture de l'interrupteur quel graphe observe-t-on ? Un ampèremètre est inséré dans le circuit. Après fermeture de l'interrupteur , l'intensité se stabilise à 1,2 A. Calculer la résistance R de la bobine. On associe en série avec la bobine B un résistor R1 =5 ohms (circuit n°2) ; un oscilloscope à mémoire est placé aux bornes de R1 . 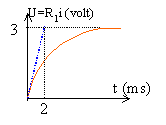- Quelle est la valeur maxi de l'intensité du courant - Quelle est la constante de temps - Calculer l'inductance de la bobine Une nouvelle bobine (L' et R') est mise en série avec r1 et un condensateur de capacité C' variable. Un générateur fournissant une tension alternative à la fréquence 5000 Hz alimente le circuit. Une voie de l'oscilloscope est branchée aux bornes de R1 tandis que l'autre est branchée aux bornes du générateur. - En examinant le graphe ci dessous, calculer la période de balayage en ms utilisée par l'oscilloscope.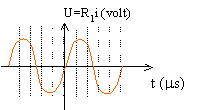 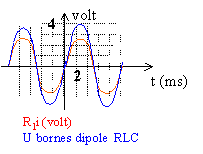- En modifiant les valeurs de la capacité, les tensions aux bornes de R1 et du générateur sont en phase (graphe ci dessous). Cet événement se produit pour C=10 microfarads. Quelles sont les valeurs de L' et R'? corrigé
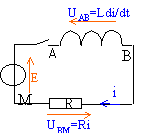
loi d'Ohm pour chaque dipole : UAM = UAB + U BM donne E = Li' + Ri (éq différentielle de l'intensité) solution proposée : i(t) = A (1- exp(-t / t)) i'(t) = A(1 / t) exp (-t / t) au bout d'un temps suffisamment long, le régime permanent est établi et l'intensité est constante, égale à : E / R la terme exp(-t / t) est nulle d'où : E / R = A. remplacer i et i' par leurs expressions dans l'équation différentielle: E = L E / R (1 / t) exp (-t / t) + R E / R (1- exp(-t / t)) E = E exp (-t / t) [ L / (Rt) - 1] +E le terme [ L / (Rt) - 1] doit être nul pour que l'égalité soit vraie d'où t = L/R constante de temps l'oscilloscope visualise la tension aux bornes du générateur de tension, interrupteur fermé ou ouvert. intensité en régime permanent : i=E/R ; 1,2 = 6 /R d'où R= 5W. l'oscilloscope à mémoire branché aux bornes de la résistance R1 donne l'image de l'intensité, au facteur R1=5 près. i max = 6 / (5+5) = 0,6 A constante de temps t2 = L / R+R1) d'où 2 10-3 = L / 10 et L = 0,02 H. le générateur impose sa fréquence (oscillateur RLC en régime forcé) période de la tension 1/ 5000 = 200ms deux sinusoïdes correspondent à 2 périodes soit 400ms dix divisions sont observées sur l'écran de l'oscilloscope : 1 div <--> 40ms. La tension observée aux bornes de R1 est l'image de l'intensité. Si intensité et tension aux bornes du dipole RL'C' sont en phase, on est à la résonance d'intensité. l'impédance du dipole est minimale, égale à la résistance totale du circuit R'+R1. d'après le graphe (R'+R1)Imax = 4 V et R1Imax = 2,5 V avec R1 = 5W. d'où : Imax = 0,5A et R'= 3 W. La fréquence du générateur est égale à la fréquence propore du dipole RL'C'. période : 2*5 =10 ms = 1 10-2 s fréquence = 100 Hz période propre du circuit RL'C' : 2p racine carrée (L'C') avec C'= 1 10-5 F (1 10-2 / 6,28)² =1 10-5 L' L' voisin 0,25 H.
2	chute d'une boule le long du mât d'un navire
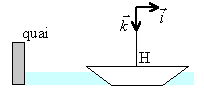
Cas du navire immobile à quai : un marin laisse tomber du haut du mât une boule sans vitesse initiale. - Étudier le mouvement du centre d'inertie de la boule dans le référentiel du navire - Déterminer la position du point d'impact dans ce référentiel - Calculer la durée de la chute. Le navire est en mouvement : le navire se déplace par rapport au quai d'un mouvement rectiligne uniforme avec la vitesse v. A l'instant origine des temps le navire est à quai et le marin lâche la boule. - Dans le repère lié au navire quelle est la trajectoire de la boule ? - quel est le point d'impact ? - Dans le repère lié au quai , quelle est l'équation de la trajectoire de la boule ? - Dans le repère lié au quai, calculer la distance parcourue par le navire et la distance horizontale parcourue par la boule pendant la durée de la chute. - Pendant cette expérience, par temps de brume intense le marin peut il savoir si le navire et en mouvement rectiligne uniforme ou au repos ? Masse de la boule 500g; hauteur du mât 20 m ; vitesse du navire 1 m/s. frottements négligés. En appliquant les lois de la mécanique classique et en faisant les hypothèses simplificatrices que l'on précisera, vérifier les deux affirmations suivantes : - Une collision à 30 km/h équivaut à une chute de 3,5 m - Une collision à 90 km/h équivaut à une chute de 32m corrigé
Pour un observateur lié au navire, le mouvement de la boule est un mouvement de chute libre verticale sans vitesse initiale. La boule tombe au pied du mât. distance parcourue : h = ½ gt² = 4,9 t² vitesse atteinte v = gt = 9,8 t ou bien v² = 19,6 h durée de la chute : racine carrée (20/4,9 ) = 2,02 s. le repère lié au navire est galiléen, tant que le navire se déplace d'un mouvement rectiligne uniforme. Le mouvement de la boule est identique à celui décrit ci dessus. Pour un observateur terrestre, la boule est animée d'un mouvement de chute libre avec vitesse initiale horizontale (1 m/s). La trajectoire est un arc de parabole; la boule tombe au pied du mât. dans un repère lié au quai : axe vertical vers le bas; origine : altitude 20 m accélération ( 0; 9,8); vitesse initiale (1; 0); position initiale (0; 0) vitesse à la date t : (1 ;9,8 t) position à la date t : x= t ; y = 4,9 t² trajectoire : y =4,9 x² durée de la chute : 2,02 s distance parcourue par le navire : 2,02 m distance horizontale parcourue par la boule = 2,02 m Le marin ne peut pas distinguer l'immobilité d'un mouvement rectiligne uniforme par temps de brume. Par contre si le navire change de direction, ou bien si le navire ralenti ou accélère, alors le marin peut distinguer l'immobilité et le mouvement . frottements négligés donc chute libre. vitesse aquise lors de la chute libre - à h = 3,5 m : v²= 19,6*3,5 et v = 8,28 m/s ou 28,81 km/h - à h =32 m : v² =19,6*32 et v= 25 m/s ou 90 km/h retour - menu