|
exercices suivants : La lune de Jules Vernes |
|
|
énergies études de courbes |
Un pendule élastique est constitué de deux ressorts de raideur k et d'un palet de masse m= 0,61 kg. Il peut osciller longitudinalement sur une table à coussin d'air horizontale. Grâce à des capteurs appropriés de position et de vitesse, reliés à une centrale informatisée, on enregistre l'évolution temporelle de l'élongation x du centre d'inertie du palet. Puis on trace les courbes qui donnent l'énergie cinétique Ec du palet et l'énergie potentielle élastique Epe du système palet et ressorts en fonction du temps t. 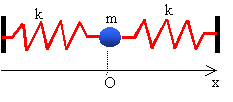 L'enregistrement a été réalisé durant 5s. L'origine de l'énergie potentielle élastique est prise à la position d'équilibre du palet (x=0). On admet que les deux ressorts sont équivalents à un ressort unique de raideur 2k. 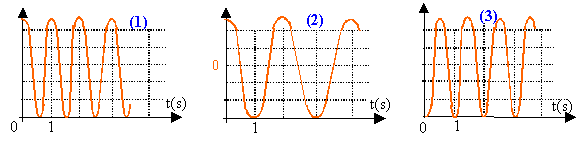
corrigé |
|
Cela est du au fait que dans le terme énergie potentielle élastique, l'élongation intervient au carré ( ½ kx²) et que dans le terme énergie cinétique, la vitesse intervient au carré ( ½ mv²) graphe 2 : élongation x(t) en fonction du temps. A l'instant t=0, 'élongation est maximale, en conséquence l'énergie potentielle élastique est maximale et l'énergie cinétique est nulle . graphe 1 : énergie potentielle élastique graphe 3 : énergie
cinétique.
période des énergies : 1 s. raideur 2k=K : période = 6,28 racine carrée (masse / raideur) élever au carré : 4 = 6,28 ² m / K d'où K= 6,28² m / 4 = 6,28²*0,61/4 = 6 Nm-1. k=3 N / m. élongation maxi : 4 cm = 2 xm d'où xm = 0,02 m. énergie potentielle élastique maximale : ½ k xm² = 0,5*6* 0,02² = 1,2 10-3 J = 1,2 mJ. l'énergie mécanique se conserve . Au passage à la position d'équilibre l'énergie est entièrement sous forme cinétique 1,2 10-3 = ½ m v ² v² = 2,4 10-3 /0,61 = 3,93 10-3 et vitesse = 6,27 10-2 m/s.
|