|
|
|
|
gravitation |
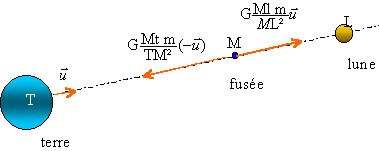
Les 3 héros ont pris place à l'intérieur d'un projectile, Colombiad, qu'un canon a propulsé en direction de la lune. On sait que l'attraction, autrement dit la pesanteur, est proportionnelle aux masses et en raison inverse du carré de leur distance. De là cette conséquence : si la terre eût été la seule dans l'espace, si les autres corps célestes se fussent subitement annihilés, le projectile d'après la loi de Newton aurait d'autant moins pesé qu'il se serait éloigné de la terre, mais sans jamais perdre entièrement son poids, car l'attraction terrestre se fait sentir à n'importe quelle distance. Mais dans le cas actuel, un moment devrait arriver où le projectile ne serait plus soumis aux lois de la pesanteur, en faisant abstraction des autres corps célestes dont on pourrait considérer l'effet comme nul. En effet la trajectoire du projectile se traçait entre la terre et la lune. A mesure qu'il s'éloignait de la terre, l'attraction terrestre diminuait en raison inverse du carré des distances, mais aussi l'attraction lunaire augmenterait dans la même proportion. Il devrait donc arriver un point où ces deux attractions se neutralisant, le boulet ne pèserait plus. Si les masses de la terre et de la lune eussent été égales, ce point se fût rencontré à une distance égale des deux astres. Mais en tenant compte de la différences des masses, il était facile de calculer que ce point serait situé aux quarante sept cinquante deuxième du voyage, soit en chiffres à soixante dix huit mille cent quatorze lieues de la terre.
Données : T est le centre de la terre et L le centre de la lune ; TL= 3,83 108 m Mt= 5,98 1024 kg ; Ml= 7,35 1022kg ; rayon terrestre Rt= 6380 km ; rayon lunaire Rl = 1740 km .On admettra que le voyage c'est le déplacement le plus court entre la surface de la terre et celle de la lune.
corrigé |
|
champ de gravitation au sol (surface de la terre) : g0 = GMt / R² ou g0R²=GMt champ de gravitation à l'altitude h: g= GMt / (R+h)² = g0 Mt R² / (R+h)² avec G : constante de gravitation et R rayon terrestre et mt masse de la terre. écrire que g/g0 = 10-4 = R² / (R+h)² prende la racine carrée des deux membres 10-2 = R/ (R+h) 0,01 (R+h) = R soit h = 0,99
R/0,01= 0,99*6380 *100 = 6,316
105 km.
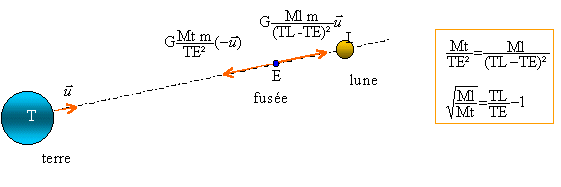
racine carré (Ml/Mt) = racine carrée (7,35 1022 / 5,98 1024 ) = 0,11 0,11 = T L/ TE -1 ou TL /TE = 1,11 et TE = TL / 1,11 = 3,83 108 / 1,11 = 3,45 108 m. remarque 52/47 = 1,06 proche de la valeur 1,11 ci dessus. |