|
concours d'entrée : technicien supérieur météo 00 |
|||
|
|||
|
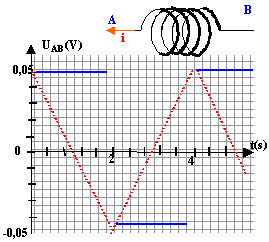
On considère une bobine d'inductance L= 5 mH et de résistance négligeable. Les variations de l'intensité en fonction du temps sont données ci-dessous : 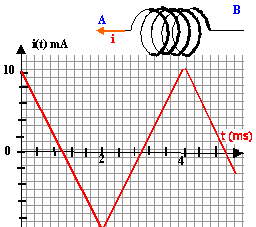
corrigé
le coefficient directeur de la droite est : - 2010-3 / 2 10-3 = -10A/s. L'ordonnée à l'origine vaut : 0,01A i(t) = -10 t + 0,01 en ampère sur [0 ; 2 ms]. sur [2 ; 4 ms] l'intensité est une fonction affine croissante ; le coefficient directeur de la droite est : 2010-3 / 2 10-3 = 10A/s. La droite passe par le point ( 2 10-3 s ; -0,01A) d'où : -0,01 = 10*2 10-3 +b soit b = -0,03A i(t) = 10 t - 0,03 en ampère sur [2 ; 4 ms]. La bobine est traversée par un courant variable : il apparaît dans la bobine le phénomène d'auto-induction électromagnétique. Une tension apparaît aux bornes de la bobine : UBA = Ldi/dt = 0,005 di/dt UBA = 0,005*(-10) = -0,05 V sur [0 ; 2 ms] soit UAB = 0,05 V. UBA = 0,005*(10) = 0,05 V sur [2 ; 4 ms] soit UAB = -0,05 V.
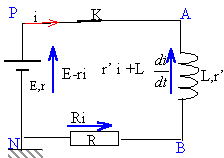
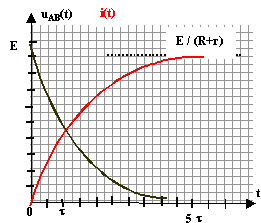
UAN=UAB +UBN d'où E-ri = Ri + Ldi/dt Li' + (R+r)i = E soit i' + (R+r) / L i = E/L on pose t = L/ (R+r) solution générale de l'équation différentielle sans second membre : i(t) = A exp ( -t/ t ) solution particulière de l'éq différentielle : quand le régime permanent est atteint i'=0 et i = E/ (R+r) solution générale de cette éq différentielle : i(t) = A exp ( -t/ t ) + E/ (R+r) A est déterminée par les conditions initiales ( t=0 et i=0) : 0 = A + E/ (R+r) donne A = - E/ (R+r) i(t) = E/ (R+r) [1-exp ( -t/ t )]. uAB(t) = L i' = L E/ ((R+r) t ) exp ( -t/ t ) = E exp ( -t/ t ).
au bout d'un temps supérieur à 5 t= 5*0,005 / 110 = 2,3 10-4 s , le régime permanent est atteint. en régime permanent : i = e/ (R+r) = 6 / 110 = 54,5 mA et uAB=0. énergie
maximale stockée dans la bobine : ½Li² =
½ 5 10-3 *0,0545² = 7,42
10-6 J.
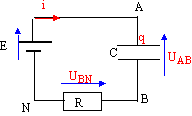
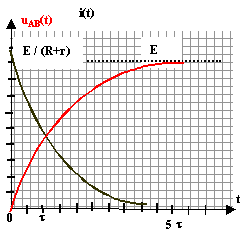
i = q' = C u'AB. UAN=UAB +UBN d'où E-ri = Ri + UAB UAB + (R+r)C u'AB= E soit u'AB + (1/ (R+r)C) UAB = E / t on pose t = C(R+r) solution générale de l'équation différentielle sans second membre : UAB (t) = A exp ( -t/ t ) solution particulière de l'éq différentielle : charge terminée UAB = E solution générale de cette éq différentielle : UAB (t) = A exp ( -t/ t ) + E. A est déterminée par les conditions initiales ( t=0 et UAB =0) : 0 = A + E donne A = - E UAB (t) = E [1-exp ( -t/ t )]. soit q = CUAB (t) et i = C U'AB. i(t) = C E/ t exp ( -t/ t ) = E / (R+r)exp ( -t/ t ).
Quand la charge est terminée, l'intensitée est nulle , qA(max) = CE = 5010-6*6 = 3 10-4 C ; qA = -qB ; énergie
emmagasinée par le condensateur en fin de charge :
½CE² = 0,5*5010-6*6² =
9
10-4 J.
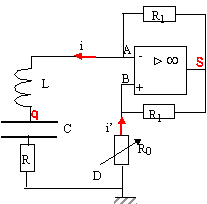
UAD = UAB + UBD = 0+ (-R0i') = R0 i. de plus UAD = Li' + q / C + Ri avec i= q' soit i' = q" Lq" + q/C+Rq' = R0 q' ou bien q" + q/(LC) + (R-R0)q'=0 si R= R0 alors l'équation différentielle s'écrit : q" + q/(LC)=0 la période des oscillations est T = 2p racine carrée (LC) = 6,28 (5 10-3 *5010-6)½ = 3,14 10-3 s. la courbe q(t) est une sinusoïde.
retour - menu |