|
concours technicien sup météo 99 |
|||
|
|||
|
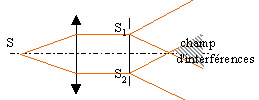
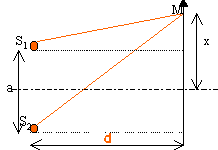
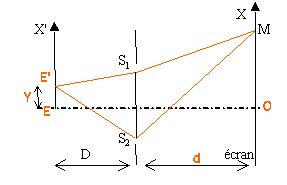
On considère un système de fentes d'Young constituées de deux fentes fines parallèles F1 et F2. Ce système est éclairé par une étoile E considérée comme ponctuelle. L'axe de symétrie du système passe par E. La lumière provenant de l'étoile étant complexe, un dispositif non représenté, permet de n'utiliser qu'une longueur d'onde l. On observe ce qui se passe sur un écran situé à une distance d= 12,5 m ( cette valeur est valable pour tout l'exercice) du centre des fentes. On appelle D la distance entre l'étoile et le plan des fentes. OM = x, l'abscisse d'un point M sur l'écran et a, la distance entre les fentes. D et d sont très grands devant a. On admet que si e est très inférieur à 1 alors (1+e)½ voisin de 1 +½e. 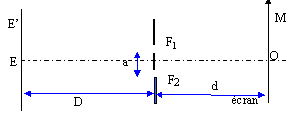
corrigé
A partir des deux fentes fines F1 et F2, on observe un phénomène de diffraction :
différence de marche d = n (S1M-S2M) . Tout le système est plongé dans le même milieu d'indice n. On supposera d >> a soit S1M + S2M voisin 2 d. S1M²=d²+(x-0,5 a)² S2M²=d²+(x+0,5 a)² S2M² -S1M² = (x+0,5 a)²-(x-0,5 a)² (S2M-S1M)(S1M+S2M) = 2 a x S2M-S1M voisin a x /d d = n a x /d = a x /d dans l'air. Si l'ordre d'interférence (p=d/l) est un entier ( la différence de marche est un multiple de la longueur d'onde), les interférences sont constructives ( franges brillantes : éclairement maximal). Si l'ordre d'interférence est égal à 2n+1 ( n entier) ( la différence de marche est un multiple impair de la demi longueur d'onde), les interférences sont destructives ( franges noires). La distance séparant deux franges brillantes consécutives est égale à l'interfrange : i =
ld/a
= 0,612 10-6 *12,5 / 1,25 = 6,12
10-6 m.
La différence de marche en M est : d' = (E'S2+S2M-E'S1-S1M)= (E'S2-E'S1) + (S2M-S1M) d' = (E'S2-E'S1) + a x /d un calcul comparable à celui ci dessus conduit à E'S2-E'S1 = a Y / D. d'où : d' = a (Y / D+ x /d ). Les nouvelles franges brillantes pour l'étoile E' sont telles que : a (Y/ D+ x /d ) = p l. Y/ D+ x /d = p l /a ou x = p l d/a - dY/D de même pour les franges noires : x = (2p+1) l d/(2a) - dY/D L'interfrange reste inchangé. La nouvelle frange centrale a une abscisse X0= - dY/D du coté opposé à l'étoile E'. Le phénomène d'interférence disparaît si la frange centrale du système d'interférence donné par E' coincide avec la première frage noire du système d'interférence donné par E. Or la distance entre la frange centrale et la première frange noire est ½ i = ½ld/a par suite ½ld/amin = dY/D amin = lD/ (2Y). la distance angulaire est Y/D soit l/(2amin )= 0,612 10-6 / (2*1,52) = 2 10-7 rad.
retour - menu |