Aurélie 05/02
dipôle (R L)

kiné Limoges 2002

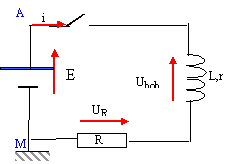
suite-->chimie : réaction prépondérante

Google

On place un conducteur ohmique de résistance R et une bobine inductive de résistance r et d'inductance L en série. A l'instant t=0 l'ensemble est soumis à une tension constante E= 4,85 V. On enregistre l'évolution des tension uR et ubob respectivement aux bornes du conducteur ohmique et de la bobine.

Etude du circuit en régime permanent :

  1. Exprimer la tension UR en fonction de r, R et E une fois le régime permanent établi.
  2. Faire de même pour la tension Ubob.
  3. Exprimer le rapport UR / Ubob en fonction de r et R. En relevant sur l'enregistrement les valeurs de ces tensions et en prenant R= 22 ohms, donner une valeur approchée de r.

Etude du circuit en régime transitoire :

  1. Etablir l'équation différentielle à laquelle obéit l'intensité. En déduire l'équation différentielle à laquelle obéit UR = f(t).
  2. Montrer que UR = E R/ (R+r) (1 - exp (-t/t)) satisfait à l'équation différentielle précédente à condition de prendre pour t une valeur qui dépend des paramètres du circuit. On donnera l'expression de t.
  3. Evaluer t à partir de l'enregistrement et en déduire L.
  4. Lorsqu'on ouvrira le circuit, une petite étincelle peut apparaître aux bornes de l'interrupteur. Pourquoi ?
    - Pour éviter cela, on place l'ensemble constitué d'une diode et d'un conducteur ohmique en parallèle avec la bobine. Faire le schéma et justifier. 

corrigé
en régime permanent ( t >4 ms) l'intensité est constante donc di/ dt = 0

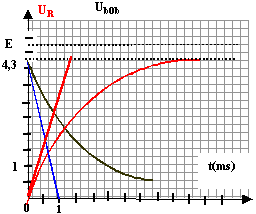
uR = Ri et ubob = ri.

de plus E = uR +ubob =Ri + ri d'où i = E / (R+r)

uR = R E / (R+r) et ubob = r E / (R+r) soit uR / ubob = R / r.

lecture graphe : uR = 4,3 ( courbe rouge ) ; ubob = 0,5 ( courbe noire)

uR / ubob = 4,3 / 0,5 = 8,6 soit 8,6 =22 / r et r = 2,6 ohms.

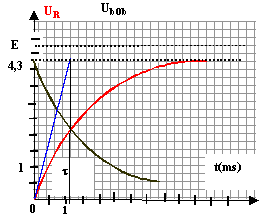
en régime transitoire ( t<4 ms) l'intensité varie.

uR = Ri et ubob = ri + L di/dt = r i + L i'.

E = uR +ubob = (R+r) i + L i'.

l'équation différentielle s'écrit : i' + (R+r)/ L i = E /L.

or uR / R = i soit i' = u'R / R

u'R / R + (R+r)/(RL) uR = E /L

u'R + (R+r)/L uR = RE /L (1)

comment trouver la constante de temps ?

à partir de uR = E R/ (R+r) (1 - exp (-t/t)) on dérive pour obtenir u'R :

u'R = E R/ ((R+r)t) exp (-t/t)

repport dans (1) :

E R/ ((R+r)t) exp (-t/t) + E R / L (1-exp (-t/t) ) = RE / L

R/ ((R+r)t) exp (-t/t) +R/L -R/Lexp (-t/t) = R/L

R / ((R+r)t) exp (-t/t)-R /L exp (-t/t) ==0

1 / ((R+r)t) = 1/L soit t = L/ (R+r).

lecture graphe : l'intersection de la tangente à l'origine ( courbe rouge) avec la droit horizontale passant par 4,3 V donne la valeur de t soit environ 10-3s.

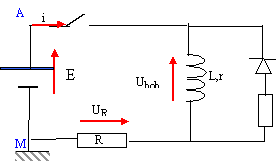
10-3 = L / (22+2,6) soit L = 24,6 mH.

On observe une étincelle de rupture à l'ouverture de l'interrupteur K car la bobine a stockée de l'énergie lors de la fermeture du circuit. En ajoutant de dispositif diode + résistor, l'énergie peut être libérée dans cette nouvelle branche (diode-résistor) ce qui évite l'étincelle aux bornes de l'interrupteur.

(La diode reste bloquée à la fermeture du circuit et ne modifie pas l'étude précédente)

 

retour - menu