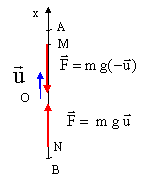Aurélie 05/02
puits diamétral dans un astre

kiné Limoges 2002

suite-->circuit RL

Google

On considère un astre sphérique de centre O, homogène, entièrement solide , de rayon R= 6000 km, de masse M= 6 1024 kg. Pour simplifier les calculs, on prendra la constante de gravitation G= 6 10-11 S.I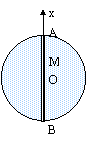

  1. Montrer que l'intensité de la pesanteur g0 à la surface de cet astre assimilé à la valeur du champ gravitationnel a une valeur très voisine de celle sur la terre.
  2. On imagine un puits diamétral AB traversant cet astre de part en part. A l'instant t=0 on abandonne en A sans vitesse initiale un objet K de masse m. cet objet tombe dans le puits où il effectue un mouvement supposé sans frottement. On le repère par son abscisse x sur un axe Ox orienté vers le haut.
    - Représenter qualitativement la force de gravitation s'exerçant sur K lorsqu'il est entre O et A, puis lorsqu'il est entre O et B.
    - En un point M de ce puits situé à la distance OM = |x| l'intensité de la pesanteur est donnée par g = g0|x|/ R. Etablir l'équation différentielle du mouvement de K.
    - Quel est le type de mouvement pris par K.
    - Etablir l'équation du mouvement x= f(t) de K sous forme littérale en fonction de R, g0 et t.
    - Calculer le temps mis par K pour aller de A en B. On prendra p² = 10 et racine carrée (6) = 2,5.
 

corrigé
g0 = GM/R² = 6 10-11 * 6 1024 / (6 106)² = 10 m/s².

écrire la seconde loi de Newton :

en M ( x>0 ) : - m g0x / R = mx"

en N (x<0) : m g0(-x) / R = mx"

d'où l'équation différentielle : mx" + m g0 / R x =0

x" + w²0x = 0 avec w²0 = g0 / R.

il s'agit de l'équation différentielle d'un oscillateur harmonique (mouvement sinusoïdal périodique).

solution générale de l'équation différentielle : x(t) = Xm cos (w0t + j)

vitesse : x' (t) = Xm (-w0) sin (w0t + j)

vitesse initiale nulle en A : x' (t=0) = 0 = Xm (-w0) sin ( j)

soit j =0 ou j = p.

j =0 conduit à : x (t=0) = R = Xm cos ( 0) = Xm ( accord avec le texte à t=0 on est en A)

j =p conduit à : x (t=0) = R = Xm cos ( p ) = -Xm ( désaccord avec le texte à t=0 on est en A et non en B)

x(t) = R cos (w0t ) avec w²0 = g0 / R.

la période est égale à : T0 = 2p/w0 = 2p/ racine carrée (R/g0 ).

la durée du parcours AB est égal à une demi-période :

p/ racine carrée (R/g0 ) = 3,14 racine carrée ( 6 106 / 10) = 2500 s.

retour - menu