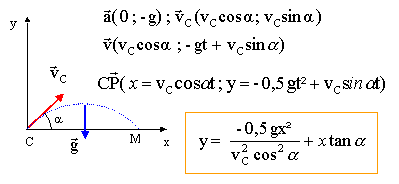Aurélie 05/02
plan incline ; piste circulaire ; chute

kiné Limoges 2002

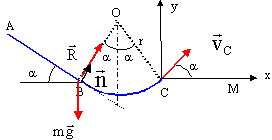
suite-->puits diamètral à travers une planète

Google

On supposera les frottements négligeables.

Un mobile K, de masse m , assimilable à un point matériel est abandonné sans vitesse initiale en A et glisse jusqu'en B le long de la ligne de plus grande pente d'un plan incliné d'un angle a par rapport à l'horizontale. On pose AB = l. Le plan incliné se raccorde tangentiellement en B à une partie cylindrique BC de rayon r. K décrit alors un arc de cercle BC, B et C étant sur la même horizontale.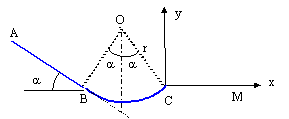

Pour les applications on prendra :

m= 0,5 kg ; g= 10m/s² ; r = 2m ; l = 7,07 m ; avec 7,07 / 10 / racine carrée (2) ; a =45° sin a = cos a = 1/ racine carrée (2).

  1. Etablir l'expression de la norme de la vitesse de K à son passage en B en fonction de l=AB, a et g. Calculer cette vitesse.
    - Caractériser le vecteur vitesse de l'objet en C.
  2. Etablir en fonction de m, g et a, éventuellement l et r l'expression de la force exercée par la piste sur le mobile en B
    - En considérant que K est toujours sur le plan incliné.
    - En considérant que K est sur l'arc de cercle.
    - Montrer que cette force subit une discontinuité dans son intensité. On calculera la valeur de sette discontinuité.
  3. Dans le repère Cxy établir en fonction de vB, g et a l'équation y = f(x) de la trajectoire de K.
    - Le mobile retrouve en M le plan horizontal passant par B et C. Exprimer en fonction de l et a la distance CM. Faire l'application numérique.

corrigé
théorème de l'énergie cinétique entre A et b: seul le poids travaille, l'action du plan étant perpendiculaire au plan

½ m v²B -0 = mgAB sina.

v²B= 2gAB sina = 2*10*7,07 * 0,707 = 100 d'où vB= 10 m/s.

le vecteur vitesse en C ( C est dans le même plan horizontale que B) :

a même norme 10 m/s ; est tangent à l'arc de cercle ; a le sens du mouvement.

sur le plan incliné en B: mg cos a = R

sur la partie circulaire en B : projeter la somme vectorielle des forces sur l'axe n du repère de Frenet

R -mg cos a = mv²B / OB= mv²B / r

R = mg cos a + mv²B / r = mg cos a + 2mgABsina/ r

discontinuité de R : 2mg ABsina / r = 25 N.

chute avec vitesse initiale :

avec v²C = 2gAB sina.

au point d'impact M l'ordonnée y est nulle :

0 = -0,5g xM² / (v²C cos²a) + xM sin a / cos a.

diviser par xM et multiplier par cos a d'où :

0,5 gxM / (v²C cosa) = sin a.

xM =2 v²C cosa sin a / g = 4 ABcosa sin² a .

application numérique : xM = 4*7,07*0,707²*0,707 = 9,9 m.

retour - menu