|
kiné Limoges 2002 |
|||
|
|||
|
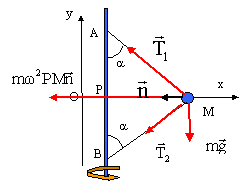
Un manège est constitué d'un axe vertical en rotation. Plusieurs nacelles sont suspendues par des tiges de longueur l =5 m qui sont articulées au sommet A de l'axe. On négligera la masse de ces tiges. Pour des raison de sécurité, un fil également de masse négligeable et de longueur l relie chacune des nacelles à la base B de l'axe de rotation. AB= 8 m. Un enfant monte dans la nacelle. On considère l'ensemble de la nacelle et de l'enfant comme un point matériel M de masse m= 40 kg. La tige et le fil lorsqu'il est tendu, font avec l'axe de rotation un angle a. Pour faciliter les calculs on prendra : g = 10 m/s² ; p² = 10 et racine carrée de 2,5 = 1,6. 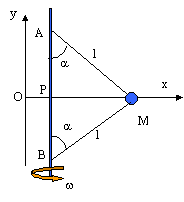
sin² a = 1- cos²a = 0,36 et sin a = 0,6.
avec PM = L sin a. Le mouvement étant uniforme, l'accélération est centripète , de valeur w² L sin a. projection de la somme vectorielle des forces sur l'axe Oy : T1cos a - T2cos a - mg = 0 (1) de même sur l'axe Ox : -T1sin a - T2sin a = -mw² L sin a T1 + T2 = mw² L (2). (1) donne : T1= T2 + mg / cos a repport dans (2) : 2T2+ mg / cos a = mw² L . T2 = ½ m[ w² L -g / cos a ] T1 = m[ w² L -½(w² L -g / cos a)] T1 = ½m[ w² L +g / cos a] application numérique :
T1 = 1236
N et T2 =
736
N.
w² L = g / (cosa ) soit w² = g / (Lcos a ) application numérique : w = 1,6 rad/s ou 0,25 tour / s.
retour - menu |