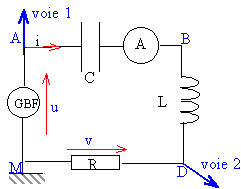
A l'aide d'un générateur basse fréquence et d'un ampèremètre, on trace la courbe de résonance d'un circuit série comprenant une bobine d'inductance L= 1 H et de résistance négligeable, un condensateur de capacité C et une résistance R .

En ordonnée, on a représenté la valeur efficace I_eff du courant et en abscisse sa pulsation w. Le générateur délivre une tension sinusoïdale de valeur efficace 1 V. On obtient la courbe suivante :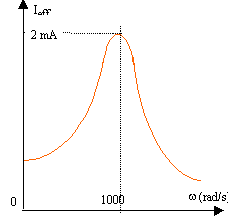

1. Représenter le montage expérimental en incorporant tous les éléments.
   - Donner les valeurs de la capacité C et de la résistance R.
2. On remplace dans le montage précédent l'ampèremètre par un oscilloscope à deux voies et à masse unique.
   - Indiquer le branchement des entrées Y₁, Y₂ pour visualiser le déphasage j de u(t) par rapport à i(t).
   - Que vaut j à la résonance ?
3. On fixe la pulsation à w = 1000 rad/s. On double la capacité du condensateur (C₁= 2C). Grâce à l'oscilloscope, on visualise les courbes représentant la tension u(t) aux bornes du générateur et la tension aux bornes de la résistance R.

   - Déterminer la sensibilité horizontale de l'oscilloscope en seconde par division sachant que l'on observe trois périodes sur l'écran de l'oscilloscope.
   - Déterminer la sensibilité verticale de l'oscilloscope en Volt par division, sachant qu'elle est identique pour les deux entrées de l'oscilloscope et sachant que l'amplitude de la tension u(t) est de 3 divisions.
   - Donner la valeur du déphasage j de u(t) par rapport à i(t) . (N'oubliez pas le signe de j ).
   - Donner l'intensité efficace du courant.

---

corrigé

---

à la résonance d'intensité LCw² = 1 avec w = 1000 rad/s et L= 1 H

C = 1/ (Lw² ) = 10^-6 F = 1mF.

à la résonance d'intensité, l'impédance Z est minimale égale à la résistance R

I_eff = 0,002 A (lecture graphe) ; R = U_eff / I_eff = 1 / 0,002 = 500 W.

à la résonance le déphasage j entre la tension u(t) et l'intensité est nul.

---

sensibilité :

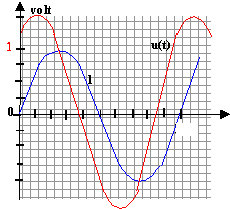
On double la capacité du condensateur :

donc la fréquence propre du dipole RLC est divisée par racine de 2 soit w₀ = 1000 / 1,414 =707 rad/s.

le GBF impose sa pulsation ( oscillations forcées) soit 1000 rad/s

fréquence : 1000 / (2p) = 159,2 Hz et période = 1/159,2 = 6,3 ms

on observe 3 périodes soit 3*6,3 = 19 ms (environ 20ms)

l'écran compte 10 divisions, la sensibilité est donc 2 ms/div.

l'amplitude de la tension u(t) est égale à la tension U_eff * racine carrée (2) donc environ 1,5 V

1,5 V pour 3 divisions ou 0,5 V/div.

---

déphasage :

la courbe (1) correspond à la tension aux bornes de la résistance R, soit l' image de l'intensité.

la courbe u(t) est en avance sur la courbe (1) d'environ 1/ 8 période ( lecture graphe)

une période est égale à 2p radians donc j voisin de p /4 ou 45°.

---

intensité efficace I_eff :

l'amplitude de la tension aux bornes de la résistance est proche de 0,9V.

0,9 = 500 I _max soit I_max = 1,8 mA

puis diviser par racine carrée de 2 soit I_eff = 1,8 / 1,414 = 1,27 mA.

---

retour - menu