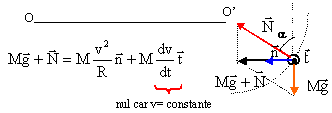Un bobsleigh (traîneau pouvant glisser à grande vitesse dans une piste creusée dans la glace) chargé de ces deux conducteurs a une masse totale M. On l'assimilera à un point matériel G. Il prend un virage ANB de rayon R et de centre O. La piste ANB est creusée dans un sol horizontal.

la coupe de cette piste par un plan vertical passant par O est un demi-cercle de rayon r <<R. G ne reste pas au fond de la piste lors de son virage, il atteint rapidement une trajectoire stable de hauteur h au dessus du fond de la piste. On veut déterminer h en utilisant les données suivantes : la vitesse v du traîneau est constante, le rayon de la trajectoire stable peut être confondu avec R, les frottements sont négligeables.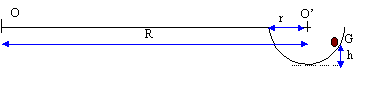

1. Préciser les caractéristiques de la trajectoire suivie par le bobsleigh.
2. Déterminer l'angle a que fait le rayon O'G de la piste par rapport à l'horizontale. En déduire la hauteur h

données : v= 30 m/s ; R= 90m ; r =2 m ; g= 10 m/s² ; cos 45 = sin 45 = 0,7 ; tan 45 = 1. 

 

---

corrigé

---

La trajectoire du bobsleigh est un demi-cercle de centre O et de rayon R+ r sin a voisin de R. La piste étant horizontale, le mouvement s'effectue dans un plan horizontal. La vitesse ayant une valeur consante, le mouvement est uniforme.

Les frottements étant négligés, l'action du sol est perpendiculaire au support. Le bobsleigh est également soumis à son poids; la somme de ces deux forces est un vecteur horizontal dirigé vers le centre du virage.

---

tan a = Mv²/R / (Mg) = v² / (Rg)

tan a = 30²/(90*10) = 1 et a = 45°.

h = r (1-cos a ) = 2*(1-cos45 )= 2*(1-0,7 )= 0,6 m.

 

pendule :

On considère un pendule simple constitué par un solide ponctuel de masse m =50 g suspendu à un fil inextensible de masse négligeable et de longueur L= 1 m. On prendra g = 10 m/s².

1. On néglige la résistance de l'air. Rappeler l'expression de la période propre T₀ de cet oscillateur. En utilisant l'étude dimensionnelle, vérifier que T₀ a la dimension d'un temps.
2. En considérant les oscillations sur un intervalle de temps relativement long, on doit tenir compte de la résistance de l'air. On le lâche sans vitesse initiale avec une amplitude angulaire a =60°. Il oscille et à cause des frottements de l'air, cette amplitude diminue. Au bout de 10 min, l'amplitude vaut a ' = 30°. Faire un schéma du dispositif et déterminer la puissance moyenne absorbée par les frottements de l'air.
3. On place sur la verticale du point d'attache O du fil, à une distance ½ L en dessous de ce point un obstacle O'. De A₁ à A les caractéristiques du pendule sont : la longueur du fil est L= 1m et l'amplitude est a . De A à A₂ les caractéristiques sont ½L et b . On néglige maintenant la résistance de l'air ( on étudie le mouvement oscillatoire pendant une période)

   - On lâche le pendule de A₁ sans vitesse initiale. Quelle est la caractéristique commune des points extrêmes A₁ et A₂.
   - Exprimer l'amplitude b en fonction de a , puis faire le calcul si a = 60°

   données : cos 60°=sin 30°= 0,5 ; sin 60° = cos 30° = 0,87.

    

---

corrigé

---

la période propre T₀ est : T₀ = 2p racine carrée (L/g)

2p est sans dimension

L est en mètre et g est une accélération en m/s² donc L/g est en s² et racine carrée (L/g) est en seconde.

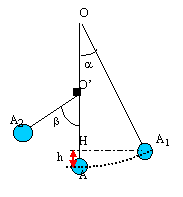
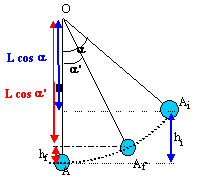
h_f -h_i= L(cosa-cosa')

au point A_i, l'énergie mécanique est sous forme d'énergie potentielle de pesanteur : mg h_i. ( origine des altitudes en A)

au point A_f, l'énergie mécanique est sous forme d'énergie potentielle de pesanteur : mg h_f.

l'énergie mécanique entre l'instant initial et la date t=10 min diminue d'une quantité égale au travail des forces de frottements

DE_m = mg( h_f -h_i)=mgL(cosa-cosa')

DE_m = 0,05*10*1 ( cos60- cos30) = 0,05*(-0,37) = - 0,0185 J

la puissance moyenne ( watt) est égale à la diminution de l'énergie mécanique (joule) divisée par le temps en seconde.

P= -0,0185 / 600 = -3,1 10^-5 W.

---

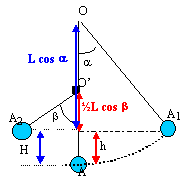
en A₁ l'énergie mécanique est sous forme d'énergie potentielle de pesanteur : mgh= mgL(1- cos a)

en A₂ l'énergie mécanique est sous forme d'énergie potentielle de pesanteur : mgH= mg ½L(1- cos b)

en l'absence de frottement l'énergie mécanique se conserve: mgL(1- cos a) = mg ½L(1- cos b)

1- cos a =½(1- cos b)

2-2cosa =1- cos b

cos b = 2cosa -1

cos b = 2 cos 60-1 = 0 d'où b =90°.

---

retour - menu