|
oxydation éthanol ( concours kiné EFOM 02) |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
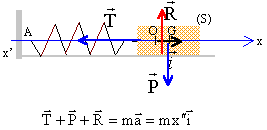
On se propose d'étudier les analogies entre un oscillateur électrique et un oscillateur mécanique. On considère les deux dispositifs suivants : - D'une part un circuit électrique comprenant, une bobine d'inductance L, de résistance nulle, un condensateur de capacité C et un interrupteur. - D'autre part un pendule élastique horizontal comprenant : un solide de masse m glissant sans frottement le long d'un axe horizontal Ox ; un ressort à spires non jointives de constante de raideur k dont l'une des extrémités est attaché au solide de masse m et dont l'autre extrémité est fixée rigidement à un support fixe. 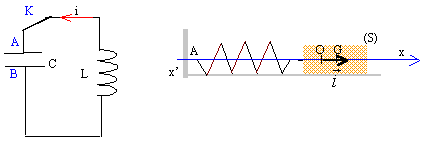 Les conditions initiales sont les suivantes : - La charge portée par l'armature A du condensateur est qA(0)= - qB(0) = Q0 positive. L'interrupteur est ouvert et on le ferme à t=0. L'intensité du courant à cet instant est i0=0. - Le mobile est initialement au repos et dans une position d'élongation maximale x0 positive. On le lâche à t=0 avec une vitesse initiale v0=0. A Etude du comportement temporel des deux modèles d'oscillateurs :
B Etude énergétique des deux oscillateurs :
C Introduction d'une dissipation d'énergie :
D Pour conclure cette étude des analogies entre un oscillateur mécanique et un oscillateur électrique, on se propose de chercher la grandeur électrique correspondant à chaque grandeur mécanique. En utilisant tout ce qui précède compléter le tableau suivant :
données : cos² x = (1+cos (2x)) / 2 et sin² x = (1-cos(2x)) / 2
tension aux bornes de la bobine ( r négligeable) : uBA= L di / dt= L i' relation entre intensité et charge : i = dqA/dt = qA' soit i' = qA'' uAB+uBA= 0 soit qA / C +L i' = 0 qA / C +L qA'' =0 ou qA'' + 1/ (LC) qA =0 avec w²=1/ (LC) solution de cette équation différentielle : qA= A cos (wt+j) à l'instant initial , la charge est égale à Q0 >0 soit Q0 = A cos j cos j = 1 soit j =0 et A = Q0 soit qA= Q0 cos (wt). période
T0 = 2p/w
= 2p
racine carrée (LC)
poids et action du support se neutralisent. d'où -kx = mx" soit mx" + kx = 0 soit x" + k/ m x =0 avec w²= k/m solution de cette équation différentielle : x= A cos (wt+j) à l'instant initial, l'abscisse est égale à x0 >0 soit x0 = A cos j cos j = 1 soit j =0 et A = x0 soit x= x0 cos (wt). période
T0 = 2p/w
= 2p
racine carrée (m/k)
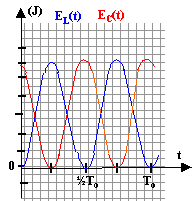
énergie stockée dans la bobine : EL= ½Li² EC+EL = constante dans la mesure où la résistance du dipole est nulle.
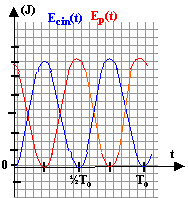
énergie potentielle élastique : EP= ½ kx² énergie cinétique : Ecin= ½mv² Ep+Ecin = constante dans la mesure où les frottements sont nuls.
uAB+uBA= 0 soit qA / C +L i' +r i = 0 qA / C +L qA'' + r qA' =0 ou qA'' + r/L qA' 1/ (LC) qA =0 si les frottements ne sont plus négligeable : -kx -lv = mx" soit mx" +lv + kx = 0 avec v = x' soit mx" + l x' + kx = 0 ou x" + l /m x' + k/m x = 0.
retour - menu |