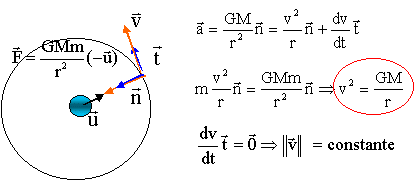Aurélie 05/02
satellite

service de santé des armées concours 2002

suite--> oscillateur mécanique

Google

Le lanceur européen Ariane a été conçu pour placer en orbite géostationnaire des satellites. Le satellite S supposé ponctuel de masse m évolue autour de la terre de masse M assimilée à une sphère homogène de centre O et de rayon R. L'étude sera effectuée dans le référentiel géocentrique considéré comme galiléen. On notera r la distance OS entre le centre de la terre et la position du satellite et on introduira le vecteur unitaire u dirigé de O vers S.

Données :

M= 6 1024 kg ; R = 6380 km ; m= 1000 kg ; r1=6700 km ; G= 6,67 10-11 m3 kg-1 s-2.

durée d'un jour T² =(24 h)² = 7,5 109 s² ; p² =10

  1. Exprimer le vecteur force d'attraction gravitationnelle F qu'exerce la terre sur le satellite en fonction de la constante de gravitation universelle G, M, m, r et le vecteur unitaire n.
    - Montrer que le mouvement du satellite sur une orbite circulaire de rayon r est uniforme. Un schéma permettra de visualiser les vecteurs force, vitesse, accélération et les vecteurs unitaires utilisés est exigé.
    - Etablir l'expression de la vitesse v du satellite sur la trajectoire circulaire de rayon r ainsi que celle de la période de révolution T autour de la terre en fonction de G, M, m et r.
  2. Qu'est-ce qu(un satellite géostationnaire ? Dans quel plan se trouve l'orbite du satellite géostationnaire .
    - Etablir l'expression r2 de l'orbite géostationnaire du satellite.
    - Déterminer numériquement l'ordre de grandeur de r2.
  3. Il serait très onéreux de propulser la fusée porteuse directement jusqu'à l'orbite géostationnaire : on procède donc par transfert d'orbites. Le satellite est d'abord placé sur une orbite basse de rayon r1 puis mené vers l'orbite géostationnaire de rayon r2 à l'aide des moteurs propulseurs. Entre les deux orbites circulaires le satellite emprunte une orbite de transfert elliptique.
    - Exprimer l'énergie cinétique Ec du satellite sur une orbite circulaire de rayon r en fonction de G, M, m et r.
    - On donne l'expression de l'énergie potentielle gravitationnelle pour le satellite situé à une distance r du centre de la terre, en choisissant l'origine de l'énergie potentielle à l'infini. Ep( r) = - GMm / r. Exprimer l'énergie mécanique Em du satellite sur une orbite circulaire de rayon r en fonction de G, M, m et r.
    - Exprimer successivement l'énergie mécanique Em et l'énergie potentielle Ep en fonction de l'énergie cinétique Ec sur cette même orbite.
    - Exprimer l 'énergie W fournie par les moteurs pour que le satellite passe de l'orbite basse de rayon r1 à l'orbite géostationnaire de rayon r2 en fonction de G, M, m, r1 et r2.
    - Calculer l'ordre de grandeur de W. 

corrigé

Au sol le champ de gravitation est égal à : g0 = GM / R² soit GM = g0 R²

G constante de gravitation; M masse de la terre et R rayon terrestre.

à l'altitude h (r =R+h) l'intensité du champ de gravitation est : g = GM/ r² = g0 R² / r².

 

le vecteur accélération est centripète ; le vecteur vitesse est tangent à la trajectoire et a le sens du mouvement

La période est la durée pour pacourir une circonférence de rayon r à la vitesse v

2pr = vT

4p²r² = v²T² = GMT² / r

T² = r3 4p²/ (GM) d'où r3 = T² GM / (4p²).

application numérique: (distance en mètre)

r3 = 7,5 109 * 6,67 10-11 * 6 1024 / (4*10) = 75 1021 d'où r = 4,2 107 m.

énergie cinétique : Ec = ½mv², remplacer v² par GM / r

Ec = ½m GM / r

énergie mécanique : Em = Ep + Ec = -m GM / r + ½m GM / r = -½m GM / r = -Ec.

énergie potentielle Ep = -m GM / r = - 2Ec.

énergie mécanique : Em(1) = -m GM / r1.

énergie mécanique : Em(2) = -m GM / r2.

W= Em(2) - Em(1) = m GM [1/ r1- 1/ r2]

l'application numérique donne ( mettre les rayons en mètres) : 2,5 1010 J.

retour - menu