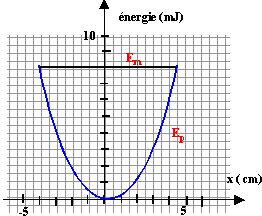
Sur un banc à coussin d'air un palet de masse m et de centre d'inertie G, est accroché à un ressort de masse négligeable, de coefficient de raideur k et de longueur à vide L₀. L'autre extrémité du ressort est fixe. Les frottements sont négligeables.

La position du centre d'inertie G est repérée par son abscisse x mesurée à partir de la position d'équilibre ( ressort non comprimé, ni allongé : x=0) Le palet est écarté de sa position d'équilibre avant d'être lâché. la durée de deux passages consécutifs de G par le point O est t = p/10 s= 0,314 s.

l'énergie potentielle de pesanteur du système {palet+ ressort + terre} est nulle.

1. Justifier l'allure des deux courbes Em(x) et Ep(x) tracées.
2. A partir de la relation liant les différentes forme d'énergie du système à une date donnée, montrer que Ep(t) est inférieure ou égale à E_m.
3. En déduire en utilisant le graphique l'amplitude X_m du mouvement de G.
4. Etablir la relation donnant l 'énergie mécanique du système en fonction de l'amplitude X_m.
5. En déduire la valeur de la constante de raideur du ressort.
6. Choisir parmi les expressions proposées ci-dessous, celle qui correspond à l'oscillateur étudié ; justifier le choix en vérifiant l'homogénéité de la formule

   T₀ =2p racine carrée (m/L₀) ; T₀ =2p racine carrée (m/k) ; T₀ =2p racine carrée (m/g) ;

7. Quelle est la valeur de la période propre T₀ de l'oscillateur ? En déduire la valeur de la masse m.
8. Le même oscillateur placé sur la lune aurait-il la même période propre ? Justifier.
9. Etablir l'expression littérale de la vitesse maximale V_m en fonction de E_m. Calculer cette vitesse.
10. Calculer la valeur de la vitesse lorsque le point G passe par le point d'abscisse x₁= -2 cm.