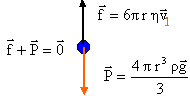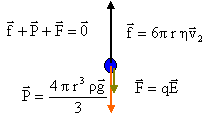Dans l'expérience de Millikan on étudie, à l'aide d'un microscope, le mouvement dans l'air d'une goutte d'huile, obtenue par pulvérisation et introduite entre les plaques horizontales d'un condensateur plan auxquelles on peut appliquer une différence de potentielle réglable V_A-V_B = U₀ positive donnant un champ électrique uniforme E.

La distance entre les plaques est d et l'intensité de la pesanteur est g.

La pulvérisation à pour effet de charger plus ou moins les gouttes par frottement. On appelle r la masse volumique de l'huile.

On observe le mouvement d'une goutte d'abord en l'absence de champ électrique puis en présence du champ électrique. On constate qu'en l'absence de champ électrique la goutte tombe verticalement et atteint très rapidement une vitesse constante v₁ que l'on mesure.

En présence du champ électrique, la goutte prend une vitesse v₂ constante de valeur supérieure à v₁, son mouvement restant vertical et descendant. On mesure la valeur v₂.

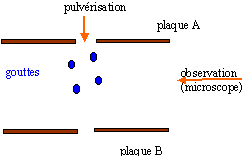Les valeurs connues au cours de l'expérience sont les constantes g, h , r ; les réglages U₀ et d ; les mesures v₁ et v₂.

L'action de l'air sur la goutte est assimilée à une force unique f de même direction que le vecteur vitesse de la goutte et de sens opposé. f = 6ph r v avec "h coefficient de viscosité de l'air" et r rayon de la goutte.

Préliminaires :

1. Lors des mesures, la goutte admet un mouvement vertical de vecteur vitesse v constant. Que peut-on dire de l'ensemble des forces qu'elle subit ? Justifier.
2. Exprimer la masse de la gouttelette supposée sphérique en fonction de la masse volumique de l'huile et du rayon de la goutte. En déduire l'expression de son poids.
3. Par analyse dimensionnelle exprimer l'unité de la viscosité h en fonction des unités de base du système international.

Etude en l'absence de champ électrique :

1. Dresser un bilan des forces exercées sur la goutte.
2. Sur un schéma soigné et légendé placer ces forces.
3. Etablir l'expression du rayon en fonction de la vitesse v₁ et des données utiles.

Etude en présence du champ électrique :

1. Sur un schéma soigné et légendé placer le champ électrique et les forces subies par la goutte. On justifiera le sens du champ électrique et celui de la force électrique.
2. En déduire le signe de la charge électrique q portée par la goutte.
3. Etablir l'expression de la charge électrique en fonction de r, v₁, v₂ et des données utiles.

Résultats :

Une série de mesures faites sur plusieurs gouttes donnent les résultats suivants pour la valeur absolue de la charge électrique des différentes gouttes

3,1 10^-19 C ; 6,4 10 ^-19 C ; 1,6 10^-19 C ; 9,6 10^-19 C ; 11,2 10^-19 C

Interpréter ces résultats.