|
suite-->acide base ( concours kiné A.P 02) |
||||||||||||||||||||
|
||||||||||||||||||||
|
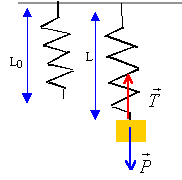
Un solide S de masse m est suspendu à l'extrémité A d'un ressort vertical de masse négligeable de constante de raideur k. Le ressort prend un allongement x0 à l'équilibre. On mesure cet allongement. A partir de cette position d'équilibre, on étire le ressort vers le bas puis on le lâche : le solide effectue alors des oscillations de part et d'autre de sa position d'équilibre. Ces oscillations se font avec une amplitude Xm et une période T0. On déclenche un chronomètre lors du passage du solide par sa position d'équilibre en repérant s'il monte ou s'il descend. On mesure la durée Dt de 20 oscillations. On répète l'expérience pour des solides de masse différente. On obtient le tableau de mesures ci-dessous. A partir de Dt on calcule T0 et T0².
On prendra p² = 10.
A la position d'équilibre poids et tension sont opposées.
kx0 = mg. Mesurer 20 oscillations est plus précis que la mesure d'une seule oscillation. L'amplitude
des oscillations diminue du fait des frottements :
l'oscillateur s'amortit.
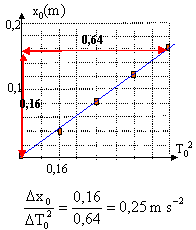
m = k / 4p² T0² représenter m = f(T0²) ; droite passant par l'origine, de coefficient directeur k / 4p² soit k/40 = 0,025k. or kx0 = mg soit m = kx0 /g kT0² = 4p²kx0 /g soit T0² = 4p²/ g x0 x0 = g/( 4p²)T0² représenter x0 = f(T0²) ; droite passant par l'origine, de coefficient directeur g / 4p² soit g/40 = 0,025g.
0,25 = 0,025 g d'où g = 10 m/s². |