Aurélie dec 2001
circuit LC

sage femme Bretagne, Normandie, Picardie 2001

exercice suivant : méthanoate d'éthyle

Google

 

  1. Un condensateur de capacité C=12,5 mF est chargé grâce à une batterie de fem E=12 V, de résistance interne négligeable (l'interrupteur K1 est fermé et K2 est ouvert).
    -Calculer la quantité d'électricité fixée par le condensateur lorsqu'il est complétement chargé et préciser l'armature qui s'est chargée positivement.
  2. Ce condensateur peut ensuite se décharger dans une bobine d'inductance L= 0,8 H supposée d'abord de résistance nulle. Pour cela à la date t=0 on ouvre K1 et on ferme K2.
    - Quelle est à la date t=0 la valeur U0 de la tension uAB et l'intensité i0 du courant dans le circuit LC ?
    - A l'instant t la tension aux bornes du condensateur vaut uC = uAB. Comment varie uC en fonction du temps ?
    - Calculer la pulsation propre w0 et la fréquence propre du circuit LC et donner l'expression de uC en fonction de t, w0 et de U0.
    - On visualise uC sur l'écran d'un oscilloscope dont le balayage horizontal du spot correspond à 5 10-3 s par cm et dont la sensibilité verticale est 6V par cm. Représenter la courbe uC que l'on observera sur l'écran de largeur 8 cm.
    - La bobine a en réalité une résistance R. Dessiner une des allures des courbes possibles que l'on pourra observer sur l'écran. Quel est le rôle de R ?

corrigé

La quantité d'électricité (coulomb) est égale au produit de la capacité (F) par la tension uAB(V) ; celle ci vaut E=12 V lorsque la charge est terminée.

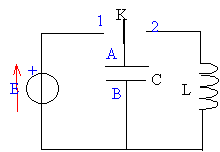
q=12,5 10-6 *12 = 1,5 10-4 C.

L'armature A du condensateur reliée à la borne positive du générateur se charge positivement, l'armature B se charge négativement.

Les deux armatures ont en valeur absolue la même charge.

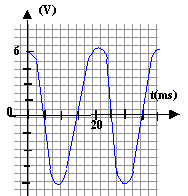
A l'instant t=0, le condensateur n'a pas eu le temps de se décharger et U0 =12 V ; l'intensité est nulle à t=0.

Il y a un échange permanent d'énergie entre condensateur et bobine inductive ; en conséquence la tension uC est une fonction sinusoïdale du temps .

pulsation :w0² = 1/ (LC) = 1 / (12,5 10-6 *0,8 ) = 105.

w0 = 316,2 rad/s.

fréquence (Hz) = 316,2 / (2*3,14) = 50,3 Hz.

uC = U0 cos (w0 t +j)

comment trouver j ? à t=0 uC = U0 d'où U0 = U0 cos (j)

soit 1 =cos (j) et j = 0

uC = U0 cos (w0 t )

la période , inverse de la fréquence vaut : 1/50 = 0,02 s =20 ms

deux périodes sont visibles sur un écran de 8 cm de large si 1 cm correspon à 5 ms.

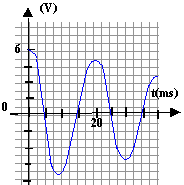
si la bobine posséde une résistance R, une partie de l'énergie est perdue sous forme de chaleur.

si R reste faible la courbe garde une allure sinusoïdale, mais l'amplitude diminue au cours du temps (régime pseudo-périodique). La résistance est la cause de l'amortissement.

retour - menu