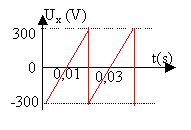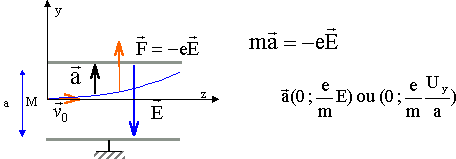Aurélie 01/02
oscilloscope

kiné Rouen 2001

exercice suivant : pendule simple

Google

 Un oscilloscope comprend une cathode C et une anode A perce d'un trou K. L'axe du tube passe par K et rencontre l'écran en O. Les plaques déflectrices horizontales Y1 et Y2 et verticales X1 et X2 sont parallèles deux à deux et distantes de a. Ce sont des carrés de côtés L. I est le centre de symétrie de la figure formée par les plaques. On pose IO=D. Les électrons émis dans le vide par la cathode C avec une vitesse pratiquement nulle sont soumis à la différence de potentiel U0= VA-VC.

Données : a= 5 cm ; L=4 cm ; D=50 cm ; U0=1500V ; m=9,1 10-31 kg ; e=1,6 10-19 C ; V0 = 2,3 107 m/s. On négligera l'effet du poids dans tout le problème.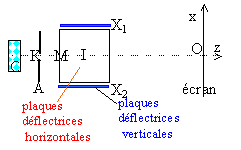

  1. Quel doit être le signe de la tension U0 pour que les électrons émis par la cathode soient accélérés. Exprimer l'énergie cinétique des électrons en K. Faire l'application numérique.
  2. Ces électrons pénetrent dans le champ électrique crée par les plaques au point M dans la direction de l'axe du tube avec la vitesse V0. La tension Ux appliquée entre les plaques verticales reste nulle et on établit entre les plaques horizontalesY1 et Y2 une tension positive Uy=Vy1-Vy2.
  3. Etablir l'équation de la trajectoire d'un électron entre les plaques dans le repère (M, z, y).
  4. On considère le point S de la trajectoire pour lequel zS=L. Exprimer l'ordonnée yS de S en fonction de U0, Uy, a et L.
    - Faire l'application numérique si Uy=150 V.
  5. Quelle est la durée du passage entre les plaques de l'électron ?
  6. L'écran de l'oscilloscope mesure horizontalement 10 cm selon l'axe (x' x) et verticalement 8 cm selon l'axe (y' y). Exprimer les coordonnées zS et yS du spot S' sur l'écran en fonction de Uy, U0, L, D et a.
    - Faire l'application numérique.
  7. On a toujours Ux=0 et on applique entre =0 et on applique entre Y1 et Y2 une tension sinusoïdale Uy=Uy1-Uy2=150 sin (100pt). Déterminer l'équation horaire de l'ordonnée du spot yS' = f(t).
    - Représenter la trajectoire en vraie grandeur.
  8. On supprime la tension Uy et on applique uniquement entre les plaques X1 et X2 une tension Ux=Vx1-Vx2 en dents de scie comme représentée ci-dessous. Donnez l'équation de Ux=f(t) pour t appartenant à [0 ; 0,02s].
  9. Donner l'équation horaire de l'abscisse du spot xS =f(t) dans ce même intervalle. Représenter la trajectoire en vraie grandeur.
  10. On établit simultanément la tension en dents de scie et Uy=150 sin (100pt).
    - Exprimer pour t appartenant à [0 ; 0,02 s] les équations horaires des coordonnées du spot xS' =f(t) et yS'=f(t)
    -En déduire l'équation de la trajectoire et la représenter en vraie grandeur.

corrigé

ce qui est écrit en bleu et en gras est un vecteur.

Le poids des électrons est négligeable et entre C et A les électrons sont soumis à la force électrique F= qE (avec q = -e)

La norme de la vitesse augmente si le travail de cette force est positif

travail de la force électrique ( de C vers A) = qUCA= eU0.

q étant négative alors UCA doit être négative ou UAC = U0 positive.

écrire le théorème de l'énergie cinétique entre le départ et K ( vitesse initiale nulle)

½mv²= eU0 = 1,6 10-19 * 1500 = 2,4 10-16 J.

vecteur vitese initiale v0 ( v0 ; 0) ;

la position initiale des électrons est l'origine du repère.

le vecteur vitesse est une primitive du vecteur accélération : v ( v0 ; eUy / (ma) t )

le vecteur position est une primitive du vecteur vitesse :

OM : z = v0 t ; y = ½ eUy / (ma) t ²

trajectoire : t = z / v0 ; repport dans y : y= ½ eUy / (ma) z² / v0² .

or m v0² = 2eU0 d'où y = Uy / (4aU0) z².

en S, sortie des plaques z =L d'où yS = Uy / (4aU0) L².

yS = 150 *0,04² / (4*0,05*1500) = 8 10-4 m.

durée de passage entre les plaques :

zS = L = v0 tS d'où tS = L / v0 = 0,04 / 2,3 107 = 1,74 10-9 s.

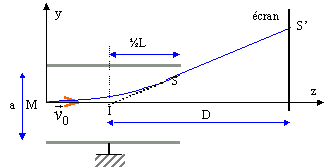
yS' / yS = D / (½L) = 2D / L soit yS' = 2D yS /L

avec yS = Uy / (4aU0) L².

yS' = DL /(2aU0) Uy = 0,5*0,04 / (2*0,05*1500) *150 = 2 cm.

il suffit de multiplier le résultat précédent par sin (100pt)

yS' = 2 sin (100pt) en centimètre.

on observe sur l'écran un petit segment vertical de 4 cm de hauteur.

on applique une tension Ux entre les deux autres plaque ( et Uy =0) ; un raisonnement identique conduira à :

xS' = DL /(2aU0) Ux = 0,5 *0,04 / ( 2*0,05*1500) Ux = 1,333 10-4 Ux .

expression de Ux en fonction du temps sur [0 ; 0,02s]

fonction affine croissante de coefficient directeur 300 / 0,01 = 3 104 Vs-1et d'ordonnée à l'origine - 300V.

Ux = 3 104 t -300 .

et xS' = 1,333 10-4 Ux = 1,333 10-4 (3 104 t -300) = 4 t -0,04

à l'instant t=0 , xS' (t=0) = -0,04 m

à l'instant t=0,02 , xS' (t=0,02) = +0,04 m

on observe un trait horizontal de 8 cm de longueur.

les deux tensions Uy et Ux existent simultanément :

xS' = 4 t -0,04

yS' = 0,02 sin (100pt) en mètre

on observe une sinusoïde, d'amplitude 2 cm, couvrant la largeur de l'écran.

retour - menu