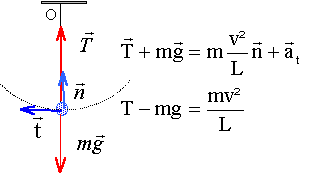|
kiné
Rouen
2001
|
|||
|
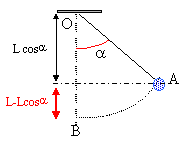
Un pendule simple est constitué d'une boule de masse M et d'un fil inextensible de masse négligeable devant M. Ce fil a pour longueur L. On note g l'intensité de la gravitation du lieu de la manipulation et a l'angle décrit par le fil et la verticale passant par la position d'équilibre du pendule.
Données : M=30 kg ; L=4m ; g=10 m/s² ; a f = 41,4° ; a i = 10° ; D t =1 min ; m=10g ; capacité thermique de l'eau c = 4,18 kJ kg-1 K-1. g= 10 m/s².
|
|||
|
T =6,28 (4 / 10)½ =
4
s.
la tension du fil perpendiclaire à la vitesse ne travaille pas de A à B travail du poids = mg L(1 -cos a ) de A à B variation d'énergie cinétique ( vitesse initiale en A nulle) : ½mv². théorème de l'énergie cinétique : ½mv² = mg L(1 -cos a ) v² = 2 gL(1 -cos a ). v² =2*10 *4( 1- cos 41,4) =
20,2 et v = 4,5
m/s.
en remplaçant v² par l'expression ci-dessus : T= m[ g + 2 g(1 -cos af )] T = mg( 3-2 cos a ) = 30*10 ( 3 - 2 cos 41,4) = 450 N.
l'énergie mécanique reste constante : ½mv² + mgL(1-cos a ) = Cte dériver par rapport au temps : (u²)' = 2uu' et (cos a )' = - sin a a' ½ m 2v v' + mgL sin a a ' = 0 v v' + gL sin a a ' = 0 or v = a ' L et v' = a '' L a '' L + g sin a = 0 si a petit alors sin a voisin de a a
'' L + g a
= 0 .
énergie potentielle initiale : mgL(1-cos af ) au bout d'un temps Dt : mgL(1-cos ai ) diminution d'énergie : |DE|= mgL(cos ai - cos af ) |DE|= 30*10*4 ( cos10-cos41,4) = 280 J énergie nécessaire pour élever une masse m (kg) d'eau de Dq degré sans chagement d'état physique : m ceau Dq = m 4180 Dq = 280 m = 0,01 kg d'où
Dq
=280 /(0,01*4180) = 6,7
°.
puissance (watt) = énergie (J) / durée (s) P = 280 / 60 =
4,67
W.
|DE| = 0,01 *4180*5,7 = 238,2 J cette énergie est perdue en 60 s soit en 60/4 = 15 périodes à chaque période, au passage au point le plus haut racourcir un peu la longueur du fil en tirant sur le fil au point le plus bas laisser le fil reprendre sa longueur initiale ( système du pendule de Compostelle)
retour - menu |