|
kiné
nantes
2001
|
|||
|
Des ions émis par une chambre d'ionisation et accélérés pénètrent dans une zone où règne un champ électrique et un champ magnétique parallèles. On négligera la force de pesanteur. Les parties 1 et 2 sont indépendantes. 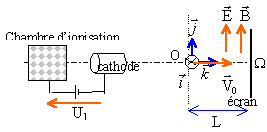 Partie1 :
Partie 2 :
corrigé |
|||
|
seule la force électrique travaille : W = q U1. DEc= ½mV²0 - ½m V²1. ½mV²0 - ½m V²1= q U1. V²0 = V²1+ 2q/m U1. V²0 mini = 2q/m U1et V²0 maxi = V²1+ 2q/m U1. Les électrons d'énergie initiale ½mV²2 ne peuvent pas atteindre la cathode si leur vitesse s'annule avant l'entrée de la cathode seule la force électrique travaille : W = -e U1 mini. DEc= 0 - ½m V²2. - ½m V²2= -e U1 mini. U1 mini = m V²2/(2e). seul le champ électrique existe :
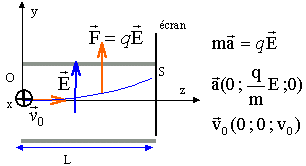
la vitesse est une primitive de l'accélération : vitesse à la date t : ( 0 ; q/m E t ; v0) le vecteur position est une primitive du vecteur vitesse : x = 0 ; y = ½q/m E t² ; z = v0 t. position des ions arrivant sur l'écran : xS = 0 ; zS = L = v0 t d'où t = L / v0. yS = ½q/m E L² / v²0. les ions décrivent un segment de droite verticale compris entre : yS mini = ½q/m E L² / v²0 maxi et yS maxi = ½q/m E L² / v²0 mini. seul le champ magnétique existe :
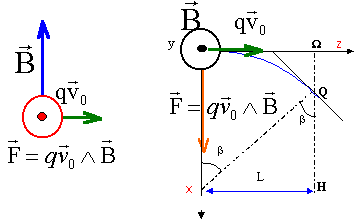
le mouvement s'effectue dans le plan défini par la vitesse et la force magnétique. Cette force est centripète ; dans la base de Frenet (suivant l'axe n) la 2ème loi de newton s'écrit : qv0B = mv²0 / R soit R = mv0 / (qB) = Cte la trajectoire est un arc de cercle. La force magnétique, perpendiculaire à la vitesse ne travaille pas ; en conséquence elle ne modifie ni l'énergie cinétique ni la norme du vecteur vitesse. Le mouvement est donc uniforme. QH =Rcos b et xQ=R - QH = R(1- cos b )= mv0 / (qB) (1- cos b ) si l'angle est petit : cos b voisin 1-½b² soit xQvoisin ½Rb². de plus on peut assimiler l'arc de cercle à la longueur L soit Rb voisin L xQvoisin ½R L² /R² = ½L² /R = qB L² /(2mv0 ) on observe un segment dont les extrémités sont : qB L² /(2mv0 maxi ) et qB L² /(2mv0 mini ) les 2 champs existent : xQ= qB L² /(2mv0 ) (1) yQ = ½q/m E L² / v²0.(2) zQ =L. (1) donne v0 = L²qB/ (2mxQ) repport dans (2) : yQ = 2E m / (LqB)² x²Q. branche de parabole.
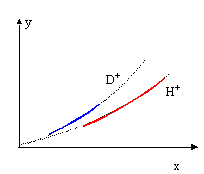
si la masse double, la charge restant inchangée : xQ (D+) = ½xQ (H+) et yQ (D+) = ½yQ (H+), la masse intervenant au dénominateur.
retour - menu |