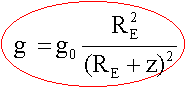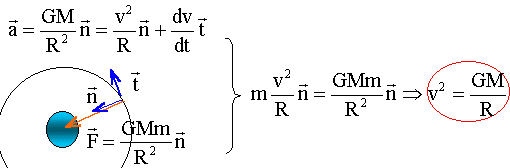Aurélie dec 2001
gravitation

Kiné Limoges 04/01

exercice suivant : bobine inductive

Google

En début de l'année 2001, une sonde américaine, après avoir été satellisée autour de l'astéroïde EROS, s 'est posée à sa surface. On frémit à la pensée que la tere puisse se trouver un jour sur la trajectoire de ce petit astre. On assimilera EROS à une petite sphère homogène de rayon RE=10 km, de masse ME = 1,5 1015 kg. L'intensité de la pesanteur au niveau du sol est : g0=4 10-3 m/s².

  1. Quelle est l'intensité de la pesanteur à l'altitude z = 30 km par rapport au sol ?
  2. Etablir brièvement l'expression de la vitesse d'un satellite de l'astéroïde supposé décrire un mouvement circulaire à l'altitude précédente. Calculer cette vitesse.
  3. Quel temps faut-il pour faire le tour d'EROS ? ( on pourra comparer ce temps à 1 jour = 86400s)
  4. La sonde spatiale arrive sur EROS à la même vitesse qu'un corps qui effectuerait un mouvement de chute libre sur la terre et qui serait parti sans vitesse initiale d'une hauteur de 5 m. Quelle est cette vitesse d'atterrissage ?
  5. Imaginons un astronaute qui, en sautant, se donne à partir du sol une vitesse v0 verticale. Sur la terre cet astronaute élève ainsi son centre d'inertie au maximum de 20 cm, avant de retomber. Pour la même valeur de v0, quelle sera l'altitude maximum atteinte si l'exercice se fait sur EROS.

     

donnée : G = 6,67 fois 10-11N.m2.kg-2. 

intensité du champ de pesanteur terrestre au niveau du sol g =10 m/s² ; on prendra racine carrée de 10 = 3,14.

corrigé

champ de gravitation à l'altitude z= 30 km :

RE = 104 m ; z = 3 104 m ; Me = 1,5 1015 kg ; g0 = 4 10-3 m/s².

g = 4 10-3 * 108 / ( 4 104)² = 4 10-3 /16 = 2,5 10-4 m/s².

vitesse à l'altitude z :

le satellite n'est soumis qu'à la force de gravitation centripète.

écrire la 2 éme loi de Newton suivant l'axe n de la base de Frenet.

avec R= RE+ z et GM = g0RE² .

g0RE² = 4 10-3 (104)² = 4 105 .

R= RE+ z = 4 104 m

v² = 4 105 / 4 104 =10 et v = 3,14 m/s.

période( s) :

le satellite parcourt la circonférence de rayon RE+ z à la vitesse v en une période T.

2p(RE+ z) = vT

T = 2*3,14 *4 104 / 3,14 = 8 104 s .

diviser par 3600 et puis par 24 : 0,925 jour terrestre.

chute libre sur terre :

l'origine des altitudes est prise au niveau du sol .

l'énergie potentiel initiale : mgh

cette énergie est sous forme cinétique lors de l'arrivée au sol

mgh = ½ mv²

v² = 2gh = 2*10 *5 = 100 d'où v= 10 m/s.

altitude maximum :

énergie cinétique initiale ½mv0²

cette énergie est convertie en énergie potentielle de pesanteur lors du saut :

½ mv0² = mghmaxi soit hmaxi = v0² / (2g)

sur terre g = 10 d'où hterre = v0² / 20

sur EROS : hEROS = v0² / (8 10-3 ) = 20 hterre /(8 10-3 )

hEROS = 2 104 / 8 hterre = 2500 hterre = 2500*0,2 = 500 m. 

retour - menu