On dispose:

- d'un point matériel M de masse m placé dans le champ de pesanteur uniforme .

- d'un ressort muni d'un plateau de masses négligeables. Le ressort est vertical et l'extrémité inférieure du ressort est fixe. Le ressort a une longueur au repos l₀, une raideur k telle que la force exercée par le ressort lorsque sa longueur est l, a pour valeur k(l-l₀).

Initialement le point matériel est en A (altitude z₀) L'altitude zéro est fixée à la cote du plateau. On lache le point matériel M. On peut décrire les mouvements successifs.

1. le point matériel descend sous l'effet de son poids (il n'y a aucune autre force qui agit sur le point)

2. Le point matériel atteint le plateau.

3. Le point matériel se déplace sous l'action de son poids et de la force exercée par le ressort . Le ressort se comprime puis revient ainsi à sa posotion de repos.

4. le point matériel "rebondit",ne se déplace que sous l'action de son poids.

On illustre les différentes étapes par les dessins suivants: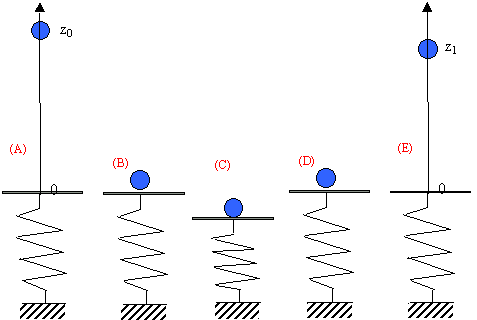

(A) : instant initial

(B) le point matériel va atteindre le plateau

(C) le ressort est comprimé au maximum

(D) le plateau est revenu à sa position initiale; le point M ne sera plus en cantact avec le plateau

(E) le point matériel atteint l'altitude z₁.

On suppose qu'il n'y a pas de perte d'énergie mécanique.

1. Exprimer la vitesse de M lorsque le point atteint le plateau.
2. Exprimer la cote la plus basse atteinte.
3. Exprimer la valeur de la vitesse de m lorsque le point quitte le plateau (situation D).
4. Exprimer l'altitude maxi z₁ atteinte (situation E)
5. En réalité dans le mouvement de B à D une partie de l'énergie mécanique est perdue.
   On donne ½ mv'_D² = e² ½mv_B², e étant le coefficient de restitution
   - Exprimer e en fonction de z₀ et z₁.
   - Enfin, après 3 rebonds, le point M atteint la cote maximale z₃. On demande e en fonction de z₀ et z₃.