|
la balançoire concours Geipi 01 exercice suivant : hydrolyse d'un ester
|
|||
|
Un enfant de masse m= 30 kg est assis sur une balançoire. On considère ce système équivalent à un pendule simple de longueur OM=3m. On choisit comme origine del 'énergie potentielle de pesanteur le plan horizontal qui contient le centre de gravité de l'enfant lorsqu'il est au repos (point S). A l'instant t=0 on propulse à la vitesse v0= 1,7 m/s l'enfant qui était au repos. 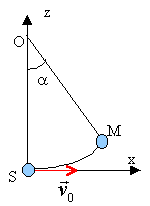
|
|||
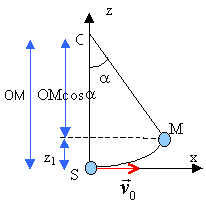
z1 = OM( 1-cosa) l'énergie mécanique se conserve : en S celle ci est sous forme cinétique : ½ mv0² en M l'énergie est sous forme potentielle de pesanteur : mgz1. ½ mv0² =mgz1. z1 = v0² / (2g) = 1,7² / 19,6 = 0,147 m.
0,147 = 3 (1-cosa) 1-cosa = 0,147 /3 =0,049 cosa = 0,951 d'où a= 18°.
période T0 :
T0= 3,47 s. la vitesse initiale étant la même et dans l'expression donnant z1, la longueur du pendule n'intervient pas. en conséquence z1=z2 = 0,147 m par contre la longueur du pendule intervient dans le calcul de l'amplitude angulaire: 0,147 = 1 (1-cosa2) 1-cosa2 = 0,147 cosa2 = 0,853 d'où a2 = 31,5°. les oscillations ne peuvent plu être considérées comme petites.
au bout de la première oscillation l'amplitude angulaire vaut : 18-0,1*18 = 16,2°. l'altitude atteinte est alors : h= 3(1-cos16,2) = 0,119 m Dh = 0,147 -0,119 = 0,0279 m énergie potentielle de pesanteur perdue : mg Dh = 30*9,8*0,0279 = 8,2 J l'énergie musculaire à fournir au cours de chaque oscillation est de 8,2 J.
retour - menu |