Aurelie 02/ 02
Concours : circuit RLC série

aide technique 2001 Poitiers

suite --> acide base

Google

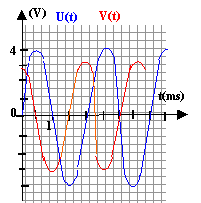
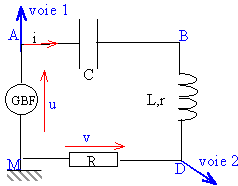
On applique aux bornes d'un circuit RLC série une tension sinusoïdale u = Um sin (2pft). On veut observer sur un oscilloscope bicourbe la tension u(t) et la tension v(t) aux bornes de la résistance R.

  1. Etablir la liste du matériel nécessaire.
  2. Représenter le circuit, les branchements de l'oscilloscope ; représenter par des flèches les tensions mesurées.
  3. Quelle relation simple relie v(t) et l'intensité i(t) ?
    - On réalise le circuit avec R= 200 W, C=22 nF et une bobine d'inductance inconnue et de résistance négligeable devant R. On obtient l'oscillogramme ci-dessous. Quelle est la fréquence de travail f ?

    - Déterminer la valeur Um et la valeur efficace Ueff.
    -Déterminer la valeur Vm et la valeur efficace Veff. En déduire la valeur de l'intensité efficace Ieff.
    - Que vaut l'impédance Z du circuit à la fréquence utilisée ?
    - Quelle est la tension en avance par rapport à l'autre ? Déterminer le déphasage.

  4. On fait varier la fréquence, Um restant constante. Pour la valeur f0 = 1250 Hz les deux courbes u(t) et v(t) sont en phase. A quel phénomène correspond cette information ?
    - Donner la relation entre L, C et f0 . Calculer la valeur de L et préciser l'unité.
    - Donner la relation entre Um et Im à cette fréquence. Que peut-on dire de Im.
  5. A coté des bornes de sortie du GBF on lit 50 W. Que signifie cette valeur ? Si on utilise le GBF pour alimenter le circuit RLC, on observe que Um diminue un peu lorsqu'on règle la fréquence. Proposer un montage très simple utilisant un amplificateur opérationnel à intercaler entre le GBF et le dipole RLC pour remédier à ce problème.

corrigé
oscilloscope ; GBF, condensateur, bobine inductive ; résistor ; fils

aux bornes du résistor tension et intensité sont proportionnelles v(t) = R i(t)

la période est voisine de 2 ms = 0,002 s (lecture graphe)

la fréquence est l'inverse de la période en seconde : f = 1 / 0,002 = 500 Hz.

Umax = 4V (lecture graphe) et Ueff = 4 / 1,414 = 2,82 V.

Vmax = 3V (lecture graphe) et Veff = 3 / 1,414 = 2,12 V.

l'intensité efficace est égale à : Veff / R = 2,12 / 200 = 10,6 mA.

La courbe rouge v(t) est en avance d'environ un quart de période (soit ½p) sur la courbe bleue u(t)

l'intensité est en avance sur la tension délivrée par le GBF

lorsque tension aux bornes du dipole RLC et intensité sont en phase :

* il s'agit du phénomène de résonance d'intensité.

* l'impédance est minimale égale à la résistance totale du dipole RLC : Umax = R Imax.

* l'intensité passe par une valeur maximale

* la fréquence du GBF est égale à la fréquence propre du dipole RLC

LCw² = 1 avec w =2pf = 6,28*1250 = 7850 rad/s

L =1 / (22 10-9 *7850² )= 0,74 henry (H)

50 W est la résistance de sortie du GBF; celui ci n'est pas un générateur parfait et la tension à ses bornes dépend du circuit réalisé à la sortie du GBF.

Un A.O montage suiveur, intercalé entre GBF et dipole RLC, permet de corriger ce probléme.

retour - menu