Les
variations de volume des calottes polaires se déduisent de mesures par
satellites de l'altitude de leur surface. le satellite Sentinel-1A
circule sur une orbite circulaire à 693 km d'altitude en passant au
dessus des pôles.
28. Calculer la valeur de la période de Sentinel-1A.
Troisième loi de Kepler : T
2 / a
3 =4
p2 / (GM).
M = 6 10
24 kg, masse de la terre ; a = R+h ; R = 6400 km , rayon terrestre.
4p2 / (GM) =4 x3,142 / (6,67 10-11 x6 1024)=9,86 10-14 ;
a3 =[(693 +6400) 103]3= 3,57 1020.
T2 =3,57 1020 x9,86 10-14 = 3,52 107 ;
T =5,9 103 s =1 h 40 min.
Sentinel-1A a un cycle de répétition orbital de 12 jours et 175 orbites par cycle.
Le satellite est muni d'un radar qui émet des ondes électromagnétiques de fréquence 5,3 Ghz.
29.
Indiquer à quel domaine des ondes électromagnétiques appartiennent ces
ondes. Citer des objets courants utilisant ce domaine de fréquence.
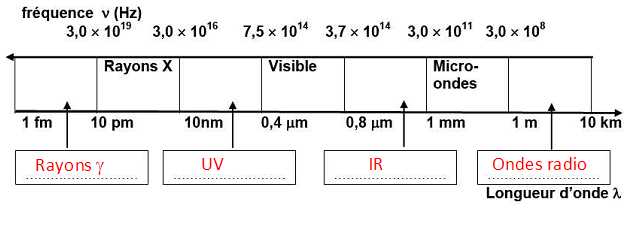
5,3 109 Hz appartient au domaine des micro-ondes.
Objets courants utilisant ce domaine de fréquence : four à micro-ondes ;
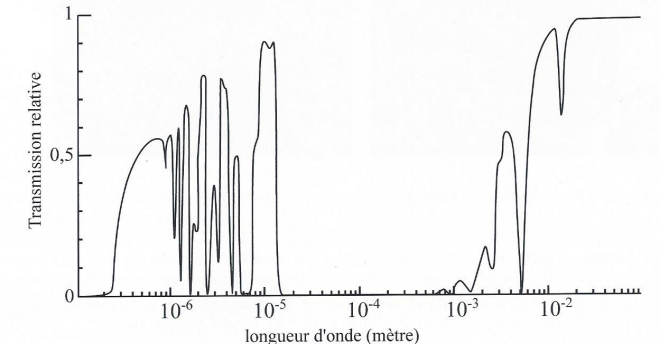
Transmission relatives des ondes électromagnétiques par l'atmosphère
terrestre. La transmission vaut 1 lorsque l'onde traverse l'atmosphère
sans subir d'absorption.
 30.
30. Justifier le choix de la fréquence du radar.
Longueur d'onde :
l = c / f =3,0 10
8 / (5,3 10
9) =5,7 10
-2 m = 5,7 cm.
Cette onde traverse l'atmosphère sans absorption.
Méthode 1 : le radar émet une onde de durée finie en direction du sol.
Cette onde est réfléchie et on enregistre l'instant auquel son écho
atteint le récepteur du radar.
31. Donner une estimation de la valeur de la durée entre l'émission de l'onde et sa réception.
Distance aller + retour / célérité = 2 x 693 10
3 / (3,0 10
8)=4,6 10
-3 s.
Le but de ces mesures est de déterminer les variations de hauteur de la
surface des inlandsis. On réitère la mesure précédente à chaque passage
du satellite au dessus du même point.
32. Définir la
résolution temporelle du récepteur du radar et calculer quelle doit
être sa valeur pour pouvoir détecter une variation de 1 cm de
l'épaisseur du glacier au niveau du point visé. Commenter.
Il faut quelques jours à un satellite pour qu'il puisse observer de
nouveau exactement la même scène à partir du même point dans l'espace.
La résolution temporelle est égale à cette période, 12 jours pour Sentinel-1A..
Méthode 2 dite interférométrique.
Elle consiste à enregistrer le décalage des oscillations de l'onde
sinusoïdale réfléchie par rapport à celle de l'onde émise, elle aussi
sinusoïdale.
Notons Ox la direction de visée. La droite Ox joint le satellite et le
point P au sol sur lequel l'onde se réfléchit. L'origine O est prise au
niveau du satellite. On note d la distance OP.
33. Sachant
que la direction de visée n'est pas nécessairement perpendiculaire à la
surface du sol, proposer une explication à l'affirmation " une zone
lisse apparaît sombre sur l'image d'amplitude ".
Une zone lisse réfléchit le signal comme un miroir ;
la
direction de visée n'est pas nécessairement perpendiculaire à la
surface du sol, le signal ne revient pas au radar. La zone lisse
apparaitra sombre sur l'image d'amplitude. Les surfaces rugueuses et
les pentes dirigées vers le satellite apparaitrons lumineuses.
L'onde émise par le satellite s'écrit : Y(x,t) = A(x) cos F(x,t) avec F(x,t) = 2p(ft -x / l).
A(x) est une fonction décroissante de x variant peu sur des longueurs de l'ordre de l.
F(x,t) est la phase de l'onde incidente sur le sol.
34. Justifier que l s'identifie à la longueur d'onde et f à la fréquence de l'onde considérée.
x / l est sans unité ; l a la même dimension que x, c'est à dire une longueur.
f t est sans unité ; f est l'invers d'un temps, donc une fréquence.
De manière analogue, l'onde réfléchie vers le satellite s'écrit : Y '(x,t) = A'(x) cos F ' (x,t) avec F ' (x,t) = 2p(f ' t +x / l ' )+ F0.
On suppose qu'à tout instant F ' (d, t) = F(d, t).
35. Exprimer f ' et l ' en fonction de f et l puis F0 en fonction de d et l.
L'onde rétrodiffusée peut avoir une amplitude variable dépendant
des propriétés du sol, mais sa longueur d'onde reste identique. à celle
de l'onde émise.
l = l '. Or l = c / f .Par suite f = f '.
F ' (d, 0 ) = 2p( d / l )+ F0. F(d,0) = 2p( -d / l).
d / l + F0 / (2p) = -d / l.
F0 = -4p d / l.
36. Exprimer la différence DF
entre la phase de l'onde réfléchie lorsqu'elle atteint le satellite et
la phase de l'onde émise par le satellite au même instant en fonction
de d et l.
DF =2p(f t +d / l )+ F0 - 2p(f t -d / l) = F0 + 4pd / l =0 si d est inchangé au cours de 2 passages consécutifs au dessus du même point..
En réalité la méthode de calcul de
DF ne donne que la valeur de
DF modulo 2
p.
Si
DF = -5p / 2 = 3p / 2 -2 x 2p, le système enregistre la valeur 3p / 2.
Si DF = -39p / 4 = p / 4 -5 x 2p, le système enregistre la valeur p / 4.
37. Calculer la valeur enregistrée par le système pour d1 = 2,85 cm , puis pour d2 = 5,6 cm et pour d3 = 6,9 cm.
l =5,7 cm ; d1 / l =0,5 ; F0 = -4p d / l =-2p, valeur enregistrée : 0.
d2 / l =0,98 ; F0 = -4p d / l = -3,92 p=0,08p-2 x 2p, valeur enregistrée : 0,08p.
d3 / l =1,2 ; ; F0 = -4p d / l = -4,8 p=1,2p-3 x 2p, valeur enregistrée : 1,2p.
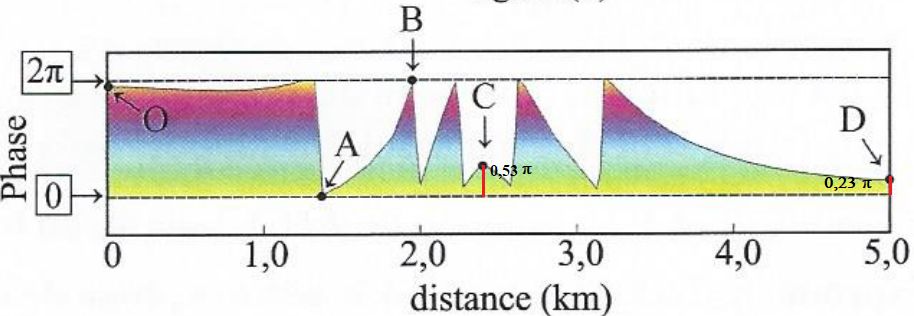
38. Expliquer la présence de discontinuité au niveau des points A et B.
 D'après la thèse de A. Augier.
D'après la thèse de A. Augier.
Le point A ne s'est pratiquement pas déplacé ; le point B s'est beaucoup déplacé.
39. Estimer la valeur de la déformation réelle ( en cm) du terrain entre les deux passages du satellite aux points B, C et D.
Point B : F0 = -4p d / l =-2p ; d / l = 2 ; d = 2 x 5,7 =11,4 cm.
Point C : 0,53 / 2 x11,4 =3,0 cm.
Point D : 0,23 / 2 x11,4 =1,3 cm.
40. Décrire
l'aspect de la figure pour une diminution uniforme de l'altitude de la
surface de l'inlandsis de 1 cm entre 2 survols successifs.
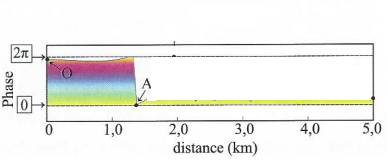
41. Commenter la sensibilité de cette méthode de mesure des variations de d.
Cette méthode est très sensible, elle permet de détecter des variations du sol de quelques centimètres.
.

 Motoneige
Motoneige


