QCM Ondes sonores, effet Doppler.
Concours audioprothèsiste Bordeaux 2017.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Une
seule réponse juste par question. Des points négatifs seront affectés
en cas de réponses fausses..
1. Déterminer la pression efficace
du signal suivant.
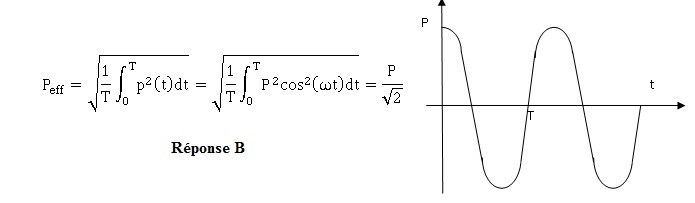
2.
Déterminer la pression efficace du signal
suivant.
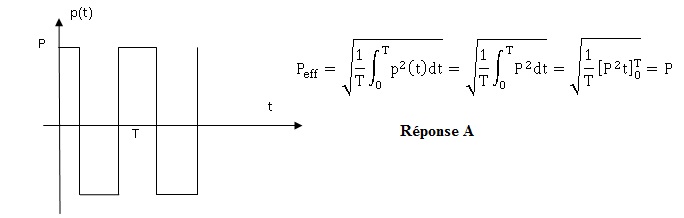
3. La
fréquence de résonance fondamentale d'une corde est donnée par : f =1/(
2 pL) (T /µ) ½
avec L : longueur de la corde ( en m) , T : tension de la corde ( N) ;
µ masse linéïque ( kg m -1).
Une corde de guitare de longueur L jouant naturellement un la de
fréquence 110 Hz est remplacée par une corde 4 fois plus légère. Sans
modifier sa tension, si on souhaite jouer la même note avec la nouvelle
corde, quelle doit être la longueur vibrante.
0,5 L ; 2L ; 0,25L ; 4 L ; 1,4
L.
µ étant divisée par 4, µ-½ est multiplié
par 2. La tension et la fréquence restant identiques, L doit être
multipliée par 2.
4. L'intensité sonore en
champ libre décroît en 1 / r2 ou r désigne la distance par
rapport à la source.
A 8 m d'un haut-parleur, l'intensité sonore vaut 3,2 mW m-2.
A quelle distance du haut-parleur devrions-nous nous positionner si
l'on souhaite un niveau sonore de 89 dB ( on suppose une propagation en
champ libre).
14 m ; 43 m ; 12 m ; 16 m ; 24
m.
I' = 10-12
x 108,9 = 10-3,1 ~7,9 10-4 W m-2
= 0,79 mW m-2.
I / I' =(r /8)2 = 3,2 /0,79 ~4,05 ; r /8 ~2,0 ; r = 16 m.
5.
On appelle niveau équivalent d'une campagne de mesures de niveaux
sonores le niveau moyen durant la dure de la campagne : L éq
= 10 log (I moy /I 0).
Concernant la campagne de mesure ci-dessous, L éq est égal
à ( en dB) :
63,6 ; 56,5 ; 54,4 ; 54,0 ; 55,1.
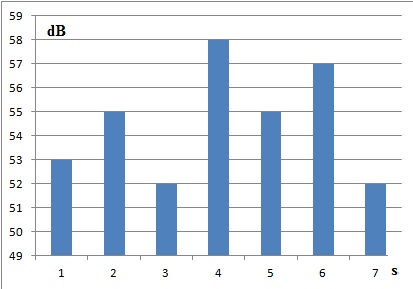 Intensité
sonore moyenne / I0=: (2,0 105+6,32 105+3,17
105 +6,3 105+5,0 105 )/ 7=3,26 105.
Intensité
sonore moyenne / I0=: (2,0 105+6,32 105+3,17
105 +6,3 105+5,0 105 )/ 7=3,26 105.
Léq = 10 log (3,26 105) =55,1.
6.
Lorsqu'on étudie le niveau sonore et qu'on souhaite avoir une
information quant à la répartition en fréquence de l'énergie, on mesure
le niveau sonore par bande d'octave. Le niveau sonore global correspond
alors au niveau de la somme des intensités dans les différentes bandes
d'octave.
Concernant la répartition par bande d'octave ci-dessous, L global
est égal à ( en dB):
69,3 ; 77,7 ; 72,6 ; 75,8 ;
462,0.
 Intensité
sonore globale / I0=: ( 106+3,16 106+2
107 +3,16 107+2,5 106 +6,3 105)/
7=5,89 107.
Intensité
sonore globale / I0=: ( 106+3,16 106+2
107 +3,16 107+2,5 106 +6,3 105)/
7=5,89 107.
Lglobal = 10 log (5,89 107) =77,7.
7.
Lorsqu'on souhaite tenir compte de la réponse de l'oreille qui n'est
pas identiquement sensible à toutes les fréquences, on applique une
correction aux niveaux sonores Li par bandes d'octave en
pondérant chaque niveau par un coefficient normalisé. L'unité devient
alors le dB(A.
Li(dBA)=Li(dB) +pondération A.)
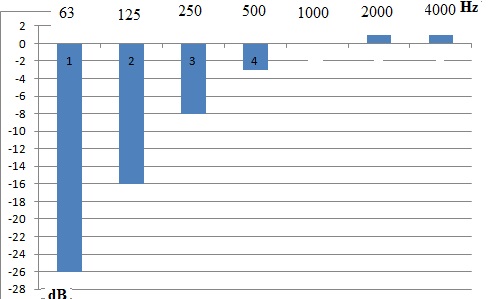
Indiquer quelle affirmation est juste.
A. Un son de 2000
Hz est perçu comme moins fort qu'un son de 1 kHz de même niveau sonore.
B. Des sons de même
niveau sonore en dB à 1 kHz et à 500 Hz sont perçus comme étant aussi
forts l'un que l'autre.
C. C'est à 1000 Hz
que nous entendons le mieux.
D. Nous sommes
sourds à 3 kHz et entendons très bien dans les graves.
E. Un son de 53 dB à 125 Hz est perçu comme équivalent en sensation de
niveau sonore à un son de 1 kHz de 37 dB. Vrai.
53-16 =37 dB(A).
8.
En tenant compte de la pondération A indiquée à la question précédente,
calculez le niveau global en dB(A) du son de la question 6:
73,2 ; 75 ; 72,3 ; 77,7 ; 411.
| Bande
d'octave (Hz) |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
| Niveau
sonore L( dB(A)) |
60-26
=34
|
65-16
=49
|
70-8
=62
|
75-3
=72
|
70 |
64+1
=65
|
58+1
=59 |
| I
/I0 =100,1 L |
2,5
103 |
7,94
104 |
1,6
106 |
1,6
107 |
107 |
3,16 106 |
7,94 105 |
Itotal /I0=3,14 107 Wm-2.
L = 10 log [ Itotal / I0] =10 log [(3,14 107)
~75 dB(A).
|
|
|
Les
questions 9 à 21 traitent de l'effet Doppler. On note :
E, l'émetteur du signal, R le récepteur du signal, c la vitesse de
propagation du signal, vE la vitesse de l'émetteur positif
si dans le sens de propagation de l'onde et vR la vitesse du
récepteur.
Le signal émis est une série d'impulsions espacées temporellement de T=
1 /f. Ces impulsions seront reçues par R avec un espacement temporel T
' = 1 /f '.
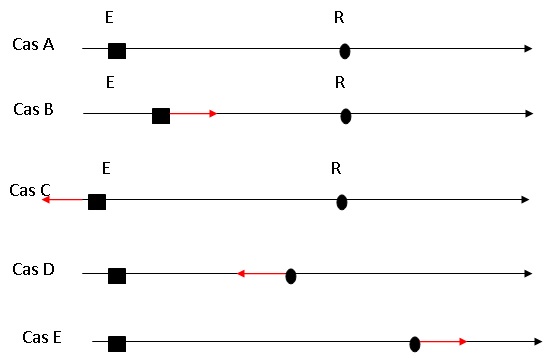
Sauf mention contraire, on considère vE << c et vR
<< c.
9. Cas B et C : E
mobile / R fixe..
Lorsqu'une impulsion arrive sur R, quelle
distance restera à parcourir à l'impulsion suivante pour arriver sur R ?
cT +vET ; cT ; cT-vET ' ; cT-vET ; cT
+vET '.
On note d la distance initiale ER et on fait l'hypothèse que d = cT.
A la date t=0, émission de la première impulsion.
A la date t=T, émission de la seconde impulsion.
Durant le temps T séparant deux impulsions successives, l'émetteur mobile parcourt la distance vET La distance séparant E et R est alors d - vET.
10. Déduisez de la question
précédente la fréquence reçue par R.
f ' = f / (1-vE/c) ; f ' = f ; f ' = f / (1+vE/c)
;f ' = f(1-vE/c)
; ;f ' = f(1+vE/c).
La seconde impulsion arrive en R à la date t' =T+(d-vET) / c.
La troisième impulsion arrive en R à la date t" =2T+((d-2vET) / c.
T ' = t"-t' =T(1-vE /c) ; f ' = f / (1-vE /c) .
11..Cas
D et E : E fixe / R mobile.
Lorsqu'une impulsion arrive sur R, quelle
distance restera à parcourir à l'impulsion suivante pour arriver sur R ?
cT +vRT ; cT ; cT-vRT ' ; cT-vRT ; cT
+vRT '.
vR est négative si R se rapproche de E.
12. Déduisez
de la question précédente la fréquence reçue par R.
f ' = f / (1-vR/c) ; f ' = f ; f ' = f / (1+vR/c)
; f ' = f (1-vR/c)
; ;f ' = f (1+vR/c).
Lorsque la seconde impulsion est émise, la première impulsion a parcouru la distance d0 = cT dans le référentiel de l'émetteur. E s'est déplacé de vET. La distance séparant deux impulsions successives est : d = (c-vE) T.
Le récepteur reçoit la première impulsion à la date t' ; il a parcouru la distance vRT ' au moment où il reçoit la seconde impulsion. Durant le temps T ' la seconde impulsion a parcouru la distance d' = d +vRT ' =cT '.
T ' = d / (c -vR) = (c-vE) T / (c-vR).
f ' = f (c-vR) / (c-vE) = f ( 1-vR /c) / (1-vE/c).
Si seul le récepteur est mobile : f ' = f (1-vR/c). Réponse D.
|
|
|
|
13. E et R mobiles.
Déduire des questions précédentes la fréquence reçue par R.
Lorsque la seconde impulsion est émise, la première impulsion a parcouru la distance d0 = cT dans le référentiel de l'émetteur. E s'est déplacé de vET. La distance séparant deux impulsions successives est : d = (c-vE) T.
Le récepteur reçoit la première impulsion à la date t' ; il a parcouru la distance vRT ' au moment où il reçoit la seconde impulsion. Durant le temps T ' la seconde impulsion a parcouru la distance d' = d +vRT ' =cT '.
T ' = d / (c -vR) = (c-vE) T / (c-vR).
f ' = f (c-vR) / (c-vE) = f ( 1-vR /c) / (1-vE/c). Réponse E.
Si seul l'émetteur est mobile par rapport au référentiel : f ' = f / (1-vE/c).
Si seul le récepteur est mobile : f ' = f (1-vR/c).
14.
Deux trains se dirigent l'un vers l'autre. Chacun roule à une vitesse
de 200 km / h. le chauffeur d'un train déclenche un avertisseur sonore
de fréquence f =750 Hz. A quelle fréquence f ' le chauffeur de l'autre
train va t-il l'entendre
?
539 Hz ; 505 Hz ; 750 Hz ; 995 Hz ; 1043 Hz.
vE = 200 /3,6 =55,5 m /s ; = vR = -55,5 m/s ; c = 340 m/s ; 55,5 / 340 ~0,163.
f ' = 750 ( 1+0,163) / (1-0,163)~1043 Hz.
.
15.
E et R sont mobiles. Supposons cette fois que le signal de fréquence f
émis par E se réfléchisse sur R et revienne sur E. En tenant compte que
lors d'une réflexion, le réflecteur se comporte comme une source,
déterminez quelle sera la fréquence f " perçue par E au retour de
l'onde. Les signes de VE et vR sont déterminés durant la phase aller.
f ' = f ( 1-vR /c) / (1-vE/c).
f " =f '( 1+vE /c) / (1+vR/c) = f ( 1-vR /c) / (1-vE/c) ( 1+vE /c) / (1+vR/c). Réponse B.
16. Un radar routier émet une onde électromagnétique de fréquence fE = 24,125 GHz. Quel est le décalage fréquentiel Df = fR-fE quand l'appareil contrôle un véhicule se dirigeant vers lui à la vitesse v = 130 km/h ; fR est la fréquence de l'onde parvenant au radar après rebond sur le véhicule.
24,125 GHz ; 2,9 kHz ; 5,8 kHz ; 25,25 GHz ; 1,125 GHz.
f " =f '( 1+vE /c) / (1+vR/c) = f ( 1-vR /c) / (1-vE/c) ( 1+vE /c) / (1+vR/c) avec vE =0.
f "= f ( 1-vR /c) / (1+vR/c) avec vR = 130 /3,6 = 36,11 m/s et vR / c ~36,11 /(3 108) ~1,2 10-7.
f " ~ f (1-2 x1,2 10-7) ; f " / f ~1-2,4 10-7 ; (f "-f) / f ~ -2,4 10-7 ; | (f "-f | ~2,4 10-7 x24,125 109 ~5,8 103 Hz ~5,8 kHz.
17.
Lorsque les mouvements de E ou R ne s'effectuent pas dans la direction
ER, seules importent les composantes des vitesses dans la direction de
propagation de l'onde ; dF est le décalage fréquentiel entre l'émission
et la réception finale.
Vémetteur : projection algébrique de la vitesse de l'émetteur ( sens + = sens de propagation du son).
Vrécepteur : projection algébrique de la vitesse du récepteur.
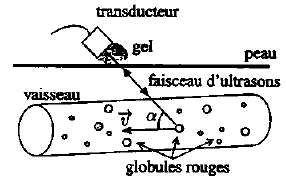
La vitesse du flux sanguin peut être déterminée à partir de la formule :
V : vitesse circulatoire : V << c. F fréquence d'émission.
V = 2c dF /F ; V = cdF / (F cos a) ;V = 2CdF/ (F cos a) ; V = CdF / F ; V = cdF / (2F cos a) vrai .
Voir un corrigé.
18. A quelle vitesse daudrait-il rouler en voiture pour qu'un feu rouge nous apparaisse vert ? lR = 680 nm ; lV = 520 nm. Il est nécessaire de tenir compte de la relativité et d'utiliser la formule : fperçu / fémis = [(1-v) / c) /(1+v /c)]½ ou c : célérité de la lumière et v : vitesse relative E / R, positive si éloignement.
220 km /h ; 260 km/h ; 230 103 km /s ; 78,6 103 km /s ; 2,83 108 km /s.
fémis = c /lR = c / 680 ; fperçu = c /lV = c / 520 ; fperçu / fémis =680 / 520 ~1,308 ; [ fperçu / fémis]2 ~1,71.
v est négative en cas d'approche : 1 +v / c = 1,71(1-v /c) ;
c+v =1,71(c-v) ; 0,71 c = 2,71 v ; v = 0,262 c =7,86 107 m/s = 78,6 103 km /s.
19. Cas B : E mobile / R fixe ( cas vE >0). f ' = f / (1-vE /c) .
Considérons un signal sonore. Que se passe-t-il si vE >c ? ( où c est la vitesse du son )
A. La fréquence augmente f ' > f et on ne doit pas considérer une formule relativiste. Vrai.
B. La fréquence augmente f ' > f et on doit considérer une formule relativiste.
C. Le récepteur ne reçoit pas de signal.
D. La fréquence diminue f ' < f et on ne doit pas considérer une formule relativiste.
E. La fréquence diminue f ' < f et on doit considérer une formule relativiste.
Voir le mur du son.
20. Cas E : E fixe / R mobile ( cas vR >0). f ' = f (1-vR/c).
Considérons un signal sonore. Que se passe-t-il si vR >c ?
A. La fréquence augmente f ' > f et on ne doit pas considérer une formule relativiste.
B. La fréquence augmente f ' > f et on doit considérer une formule relativiste.
C. Le récepteur ne reçoit pas de signal. Vrai.
D. La fréquence diminue f ' < f et on ne doit pas considérer une formule relativiste.
E. La fréquence diminue f ' < f et on doit considérer une formule relativiste.
21. Cas E : E mobile / R fixe ( cas vE >0). f ' = f / (1-vE /c) .
Considérons un signal lumineux. Que se passe-t-il si vE >c ? ( où c vitesse de la lumière )
A. La fréquence augmente f ' > f et on ne doit pas considérer une formule relativiste.
B. La fréquence augmente f ' > f et on doit considérer une formule relativiste.
C. C'est impossible. Vrai.
D. La fréquence diminue f ' < f et on ne doit pas considérer une formule relativiste.
E. La fréquence diminue f ' < f et on doit considérer une formule relativiste.
|
|