.
|
|
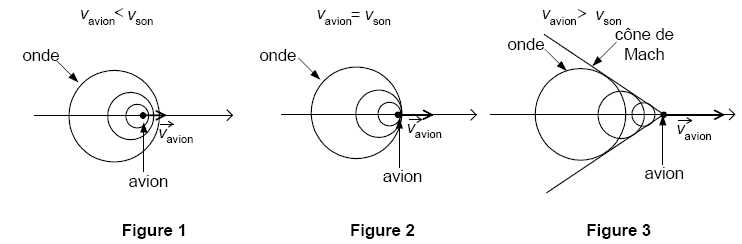
Lorsqu’un
avion vole en vitesse subsonique (vitesse inférieure à la célérité du
son dans l’air), il crée des ondes dites de pression qui se propagent à
la célérité du son (figure 1). Lorsqu’il accroît sa vitesse et qu’il
atteint la célérité du son, les ondes de pression s’accumulent devant
le nez de l’avion (figure 2). Lorsqu’il dépasse la célérité du son (on
dit qu’il passe le mur du son), il se produit alors des ondes de
compression et de dilatation qui provoquent ce fameux « bang »
perceptible à plusieurs dizaines de kilomètres à la ronde. Pour une
vitesse supérieure à la célérité du son, les ondes se propagent
derrière l’avion dans un cône appelé cône de Mach.
Aussi incroyable que
cela puisse paraître, c’est le même phénomène de passage du mur du son
qui explique le claquement produit par un coup de fouet.
Étude des ondes sonores.
Dans cette partie, les ondes sonores se propagent dans l’air.
Quelques caractéristiques des ondes sonores.
Pourquoi peut-on dire qu’il s’agit d’ondes mécaniques ?
Les ondes sonores, comme les ondes mécaniques, ne se propagent pas dans le vide. Elles se propagent dans u milieu matériel.
Choisir
la (ou les) bonne(s) caractéristique(s) qui qualifie(nt) une onde
sonore, en expliquant la signification des caractéristiques
choisies :
a) progressive b) tridimensionnelle c) transversale d) longitudinale.
Les
onde sonores sont des ondes progressives tridimensionnelles
longitudinales : elles se propagent à partir de la source
dans toutes les directions qui lui sont offertes ; la direction de la
perturbation est parallèle à la direction de propagation de l'onde.
Choisir dans la liste le (ou les) «milieu(x)» dans lequel le son ne se propage pas :
a) acier b) béton c) vide d) eau.
Le son se propage dans un milieu matériel, acier, béton, eau. Le son ne se propage pas dans le vide.
Ondes sonores produites par un avion.
Un avion vole à la vitesse vavion = 800 km.h-1
à une altitude d’environ 10 km. On veut savoir s’il se déplace à une
vitesse supérieure à la célérité du son sachant que cette dernière
dépend de la température.
La célérité du son peut se calculer en première approximation par la relation :
vson (q) = vson(0°C) (1 + q/273)½.
avec q la température en degré Celsius et vson (0°C) = 3,3 102 m.s-1.
Calculer la célérité des ondes sonores à l’altitude de 10 km en considérant que la température q de l’air vaut - 50°C.
vson (-50) = 3,3 102 (1 -50 / 273)½ = 298,25 ~3,0 102 m/s.
Comparer cette valeur avec la vitesse de l’avion. Celui-ci a-t-il passé le mur du son ?
298,25 *3,6 = 1074 ~1,1 103 km / h.
La vitesse de l'avion est inférieure à la vitesse du son : l'avion n'a pas dépassé le mur du son.
|
.
Le claquement d’un coup de fouet.
Un
artiste de cirque veut faire claquer son fouet ; pour ce faire, il
génère, d’un mouvement de poignet, un ébranlement qui se déplace à la
célérité v le long de la lanière en cuir du fouet.
Cette célérité v
dépend de la tension F de la lanière et de sa masse linéique μ (masse
par unité de longueur) suivant la relation : v = (F / µ)½.
Montrer, par une analyse dimensionnelle, l’homogénéité de cette relation.
F est une force exprimée en newton, c'est à dire une masse fois une accélération : [F] = M L T-2.
µ est une masse par unité de longueur : [µ] = M L-1.
[ F / µ] = L2 T-2 ; [ (F / µ)½]= L T-1, c'est à dire la dimension d'une vitesse.
On
simule à l’aide d’un logiciel la propagation de la perturbation le long
de la lanière et on obtient la position de l’ébranlement à différentes
dates séparées d’un intervalle de temps Dt = 3,5 10-2 s.
La lanière du fouet a une longueur L = 3,0 m.
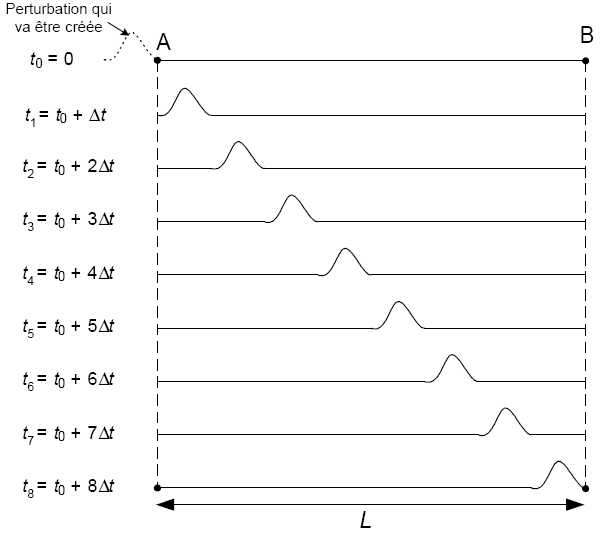
Calculer la durée t mise par l’onde pour parcourir toute la lanière.
t = 8 Dt = 8*3,5 10-2 =0,28 s.
En déduire la valeur de la célérité v de l’onde.
v = L / t = 3,0 / 0,28 = 10,714 ~ 11 m/s.
En
réalité, la section de la lanière du fouet diminue au fur et à mesure
que l’on s’éloigne de la poignée ; la masse linéique μ diminue donc. Si
on suppose que la tension F est constante,
comment évolue la célérité de l’onde le long de la lanière, de la poignée à son extrémité ?
La célérité est inversement proportionnelle à la racine carrée de la masse linéïque : si µ diminue, alors la célérité augmente.
On s’intéresse maintenant à la vitesse de déplacement transversal de la mèche qui correspond à l’extrémité du fouet.
On
enregistre son mouvement avec une caméra ultra-rapide. La fréquence de
prise de vue est de 4000 images par seconde. Entre deux images
successives, la mèche, du fait de la propagation de la
vibration, se déplace d’une distance d = 11 cm (voir figure 5).

En déduire la vitesse v’ de déplacement de la mèche. Dans ces conditions, le mur du son a-t-il été passé par la mèche ?
Donnée : célérité du son dans l’air à 20°C : vson = 340 m.s-1.
Durée séparant deux images successives T = 1/4000 s.
v' = d / T = 0,11 *4000 = 440 ~ 4,4 102 m/s.
v' est supérieure à la célérité du son : le mur du son a été dépassé.
|
|
|


