Physique
chimie, mise en mouvement de la table d'harmonie, concours g�n�ral 2020.
Jouer du violon
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
..
..
|
.
.
|
..
..
......
...
|
Une
partie de l'�nergie de la corde est transmise � la table d'harmonie via
le chevalet, pour que la table d'harmonie puisse rayonner une onde
acoustique. Le chevalet est mis en mouvement sous l'effet de la
projection Fy sur l'axe horizontalde la tension de la corde, de norme F0.
le chevalet met � son tour la table d'harmonie en mouvement. Plus les
d�formations de la table d'harmonie sont importantes et plus le son
�mis par le violon est puissant.
On propose d'estimer l'ordre de grandeur de la force Fy que la corde
exerce sur le chevalet. On consid�re que la d�formation de la corde
obtenue lorsque le coin de Helmholtz P se trouve sous l'archet, ce qqui
correspond � la configuration suivante.
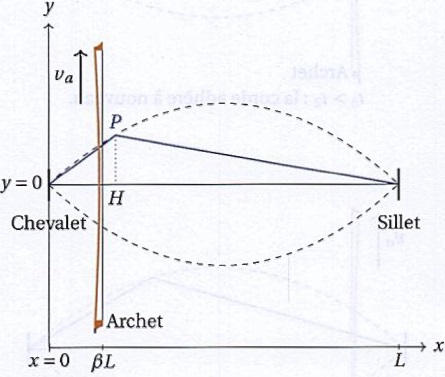
59. Etablir la relation Fy ~F0 va T/ (2L)(1- �) / �.
On se trouve entre les phases de glissement et d'adh�rence ; l'amplitude est maximale.
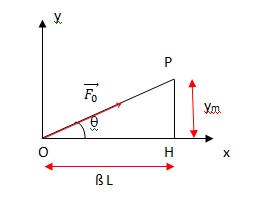
En projection sur l'axe des y : Fy = F0 sin q.
tan q = ym /(�L).
Pour les petits angles : sin q ~ tan q ~ ym /(�L).
Or, d'apr�s la question 44, ym = 0,5 va T(1-�).
Par suite : Fy ~F0 va T/ (2L)(1- �) / �.
60. Faire l'application num�rique et commenter. F0 = 51,2 N ; va = 0,20 m /s et � =0,10.
Fy ~51,2 x0,20 x 3,4 10-3/ (2 x 0,33) x0,9 / 0,1 =0,47 N.
Cette valeur est 100 fois plus faible que la force de tension.
61. Comment le violoniste peut-il parvenir � prodiuire un son puissant ?
L'intensit� de la force d�pend de la vitesse de d�placement de
l'archet. En d�pla�ant rapidement l'archet, le son est plus puissant.
Le diagramme de Schelleng indique pour une vitesse d'archet donn�e, la
zone � l'int�rieur de laquelle le mouvement de Helmholtz est atteint.
La force relative correspond au rapport de la force appliqu�e par le
violoniste sur l'archet � la force la plus grande qu'on puisse
appliquer � la vitesse d'archet donn�e.
62. Expliquer pourquoi seuls les violonistes chevron�s jouent du violon en frottant l'archet � proximit� du chevalet.
La zone " son brillant " est d'autant plus �toite que l'on se trouve
proche du chevalet. Obtenir un son brillant, avec un archet proche du
chevalet, demande donc une grande pr�cision sur la force �
appliquer.
|
...
|
....
|
La
vibration de la table d'harmonie d�termine la richesse du son produit.
La vibrom�trie laser permet au luthier d'optimiser la table d'harmonie.
Le vibrom�tre laser est constitu� d'une source lumineuse
monochromatique, d'un interf�rom�tre et d'un d�tecteur. Le faisceau
�mis par le laser est s�par� dans l'interf�rom�tre en un faisceau de
r�f�rence ( dirig� vers le d�tecteur) et un faisceau de mesure ( dirig�
vers un point de la table d'harmonie). Ce dernier est r�fl�chi par la
table d'harmonie. Une partie de la lumi�re r�fl�chie revient alors dans
l'interf�rom�tre o� elle interf�re avec le faisceau de r�f�rence. Gr�ce
� ce dispositif, on parvient �mesurer des vitesses qqui s'�chelonnent
de 0,01 �m /s � quelques dizaines de m�tres par seconde.
On mod�lise le faisceau de r�f�rence par une onde lumineuse � laquelle on associe un signal sinuso�dal de fr�quence f0.
Du fait du mouvement local de la table d'harmonie � une vitesse v,
l'onde lumineuse r�fl�chie est associ�e � un signal sinuso�dal de
fr�quence fr diff�rente de f0 : fr = f0 +df avec df = 2f0v /c.
L'analyse de l'�tat d'interf�rence de ces deux signaux fournit � une
mesure de la vitesse locale v de vibration de la table d'harmonie. Le
balayage de toute la surface du violon nous renseigne alors sur le mode
de vibration de la table d'harmonie.
63. Dans ce laser
h�lium n�on, la radiation amplifi�e correspond � une transition
�lectronique enttre deux niveaux d'�nergie de l'atome de n�on. La
longueur d'onde de cette radiation est l0
= 633 nm. En d�duire la valeur num�rique de la diff�rence d'anergie (
en eV) entre les deux niveaux d'�nergie concern�s. Quelle est la
couleur de la lumi�re �mise par ce laser ? Quelles propri�t�s du
rayonnement laser sont mises � profit dns cette technique.
E = hc / l0 =6,63 10-34 x3,00 108 /(633 10-9) =3,14 10-19 J
soit 3,14 10-19 / (1,60 10-19) ~ 1,96 eV.
633 nm correspond � une lumi�re rouge.
La lumi�re laser est coh�rent, tr�s directionnel, et transporte beaucoup d'�nergie par unit� de surface.
64. Nommer l'effet � l'origine du d�calage de fr�quence. Citer d'autres situations o� cet effet intervient.
Il s'agit de l'effet Doppler-Fizeau.
Cont�le de la vitesse des voiture par radar ;
Perception diff�rente de la sir�ne d'une voiture lors de l'approche ou de l'�loignement d'un observateur.
La figure suivante donne l'�volution temporelle du signal lumineux de r�f�rence s0(t), du signal lumineux r�fl�chi sr(t) et du signal r�sultant de leur interf�rence s(t) = s0(t) + sr(t).
On constate que p�riodiquement, l'interf�rence des deux signaux
est constructive et conduit � un signal r�sultant d'amplitude maximale.
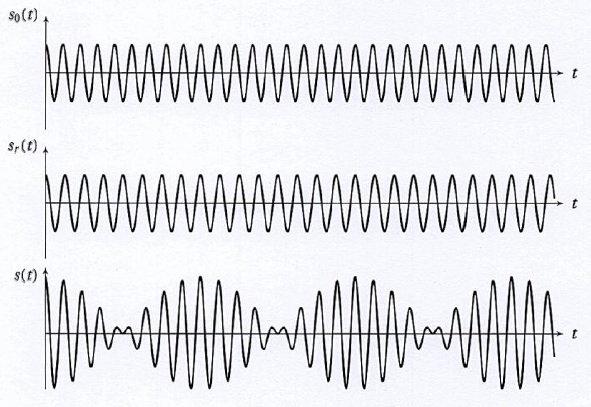
65.
Exp�rimentalement, on d�termine que les interf�rences constructives se
r�p�tent avec une p�riode �gale � 97,25 �s. En d�duire la valeur de la
vitesse de vibration locale v de la table d'harmonie.
Dans un souci de simplicit� s0(t) = sm cos ( 2 p f0 t) et sr(t) =sm cos ( 2 p fr t).
s(t) = s0(t) + sr(t).
s(t) = sm [cos ( 2 p f0 t) +cos ( 2 p fr t)]
s(t) = sm [cos ( p (f0 +fr)t) +cos ( p (f0 -fr)t)].
s(t) = sm [cos ( p (2f0 +df)t) +cos ( p df t)].
Le premier terme correspond � la variation rapide, ressemblant � celle des signaux d'origine.
Le second terme correspond � la variation plus lente de p�riode 2 T
p df T = 2p ; df T = 2 ; 2f0v /c T =2 ;
v = c / (f0 T)= l0 / T =633 10-9 /(97,5 10=6,5 10-3 m /s = 6,5 mm /s.
|
|
