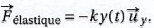Physique
chimie, jouer du violon, portrait de phase, concours général 2020.
Huile de lin  Mouvement de la table d'harmonie. Mouvement de la table d'harmonie.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
.
.
|
..
..
......
...
|
1. Le
mouvement de Helmholtz ( noté mdH).
C'est le mouvement que le violoniste doit chercher à reproduire pour
obtenir un son de qualité.
On considère une corde de longueur L, tendue entre deux extrémités
fixes. Le contact entre l'archet et la corde s'effectue en un point M,
supposé ponctuel, situé à l'abscisse ß L ( 0 < ß < 1) comptée depuis
l'extrémité de la corde fixée au chevalet. L'archet se déplace
perpendiculairement à la corde à la vitese va,
constante, par rapport au violon. Helmholtz a observé que la corde peut
être décomposée en deux segments de droite reliés en un point P, appelé
coin de Helmholtz.
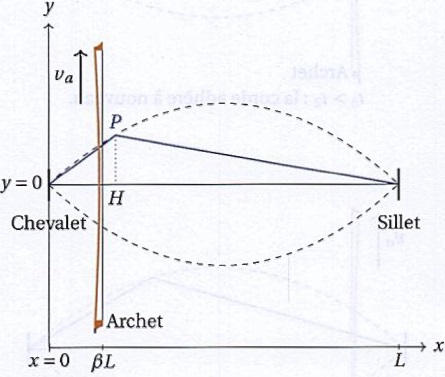
D'un point de vue cinématique, la projection du coin P sur l'axe de la
corde au repos, notée H, fait des allers-retours à la vitesse co
entre les extrémités de la corde. Ce mouvement est périodique, de
période T = 2 L / co. On peut montrer que la trajectoire du
coin de Helmholtz P est constitué de deux arcs de parabole représentés
en tirets.
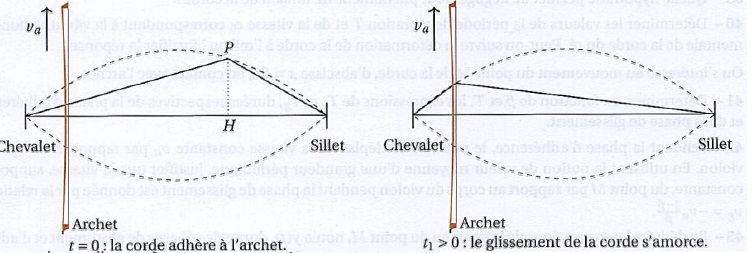
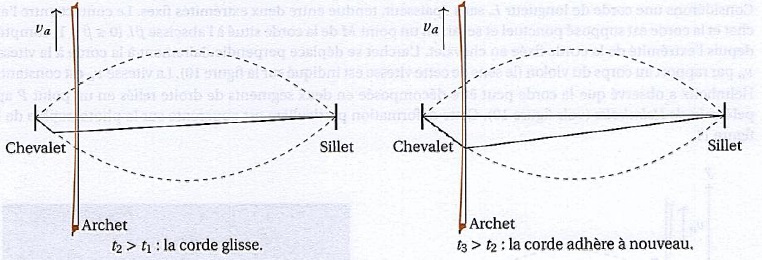
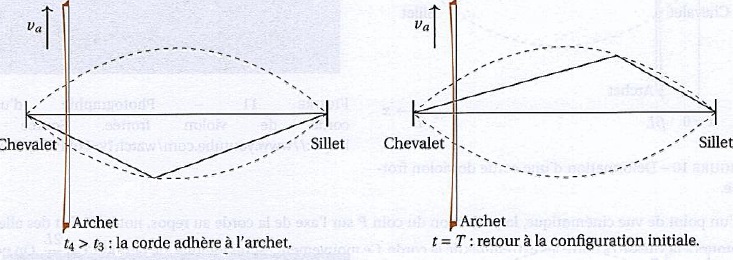
Lorsque l'archet frotte la corde, cette dernière adhère à l'archet
pendant la durée où le point H est situé entre l'archet et le sillet.
Lorsque le point H est situé entre le chevalet et l'archet, la corde
glisse sur l'archet. La figure suivante représente quelques états
successifs de la corde au cours d'une période du mouvement de Helmholtz.
38. Les ondes de
déformation de la corde peuvent-elles être qualifiées de longitudinales
ou transversales ?
La déformation de la corde se fait perpendiculairement à l'axe de la
corde. Il s'agit d'ondes transversales.
39. Quelle
hypothèse permet de négliger tout phénomène de torsion de la corde ?
Hypothèse : la corde est supposée dans épaisseur ; elle ne peut donc
pas tourner sur elle même.
40. Déterminer les
valeurs de la période de vibration T et de la vitesse c0
correspondant à la vibration fondamentale de la corde du ré.
Peut-on suivre la déformation de la corde à l'eoil nu ? Justifier.
La corde du
ré a un fondamental de fréquence f = 294 Hz.
T = 1 / f = 1 / 294 ~ 3,40 10-3 s = 3,40 ms.
co = 2L / T = 2Lf = 2 x0,33 x 294 ~1,9 102 m /s.
L'oeil humain peut distinguer des féquences allant jusqu'à 10 Hz ( 10
images par seconde). Cet oeil ne peut donc pas suivre la déformation de
la corde.
On s'intéresse au mouvement du point M de la corde, d'abscisse ßL, en
contact avec l'archet.
41. Déterminer en
fonction de ß et T, les expressions de Ta et Tg, durées respectives de
la phase d'adhérence et de la phase de glissement.
Phase d'adhérence : H est situé entre archet et sillet. H
effectue un aller-retour entre archet et sillet, de longueur
L(1-ß).
Ta = 2L(1-ß) / co = (1-ß)T.
Phase de glissement : durée de l'aller retour entre archet et
chevalet de longueur ßL.
Tg = 2ßL / co = ß T.
42.
Pendant la phase d'adhérence, M se déplace à vitesse constante va
par rapport au corps du violon. En utilisant la notion de valeur
moyenne d'une grandeur périodique, justifier que la vitesse, supposée
constante, du point M par rapport au corps du violon pendant la phase
de glissement est donnée par : vg = -va ( 1-ß) /
ß.
Le mouvement de la corde
est périodique de période T.
adhérence : M parcourt la distance da à la vitesse va
;
da = va Ta = va (1-ß)T.
Glissement : dg = vg Tg
= vg ßT.
Le point M revient à sa position initiale : da
+dg=0 ;
va (1-ß)T +vg ßT = 0 ; vg = -va ( 1-ß) / ß.
43. En déduire les
expressions de la position du point M, notée y(t), durant chaque phase
en considérant que le mouvement commence à la date t=0 par une phase de
glissement avec y(0) = 0.
A t=0, M est à la position d'équilibre, donc à la moitié de la phase de
glissement.
Pour 0 < t < 0,5 Tg :
y(t)=vgt = -va ( 1-ß) / ß t.
La phase d'adhérence débute à t = 0,5Tg.
y(0,5Tg) =-0,5va (
1-ß) / ß Tg =0,5va ( 1-ß) T.
Pour 0,5 Tg <
t < T-0,5 Tg
, il y a adhérence.
y(t) = va(t-0,5 Tg)-0,5 va (1-ß)T =vat
-0,5va( Tg+(1-ß)T) =vat -0,5va(
ßT+(1-ß)T)=va(t-0,5 T).
La dernière partie du mouvement est un glissement pendant t -(T-0,5 Tg)..
T-0,5 Tg <
t < T : y(t)=vg
(t-(T-0,5 Tg)+0,5vaT(1-ß) =vgt+ vgT(1-0,5
ß)+0,5[-vg
ß /(1-ß)]T(1-ß).
y(t)=vgt+vgT(1-0,5
ß)-0,5vg ßT=vgt+vgT(1-ß).
44. Montrer que
l'amplitude de la déformation maximale ym de la corde à
l'abscisse du point M s'écrit :
ym = 0,5 vaT(1-ß).
y varie de façon affine entre les deux valeurs extrèmes -0,5 va
T(1-ß) et 0,5 va T(1-ß).
Amplitude de la déformation maximale de la corde en M : ym = 0,5 vaT(1-ß).
45. Calculer ym
pour la corde ré du violon avec va = 0,20 m /s et ß = 0,10.
Commenter.
ym =0,5 x0,20 / 294 x(1-0,10) ~3,8 10-4 m= 0,38
mm, invisible à l'oeil nu.
La figure suivante représente y(t) d'une corde de violon pour
différentes valeurs de la vitesse va.
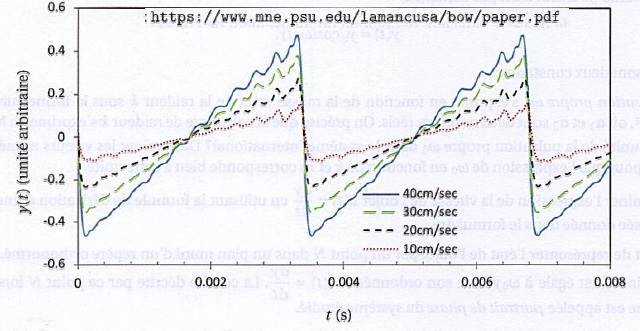
46. Commenter
l'allure expérimentale de l'élongation y(t) de la corde. Commenter
l'influence de la vitesse de l'archet sur cette élongation.
Aux variations linéaires du modèle de
Helmholtz se superposent d'autres variations dues à la présence
d'harmoniques dans un son complexe.
La vitesse de l'archet influe uniquement sur l'amplitude de
l'élongation ( intensité du son émis), mais pas sur sa forme.
|
...
|
....
|
2.Un
modèle d'oscillations entretenues.
Afin d'interpréter l'alternance de sphases d'adhérence et de glissement
de la corde sur l'archet, on propose le modèle suivant.
Un objet, de masse m, repose sur un tapis roulant. Cet objet est relié
à un point fixe par l'intermédiaire d'un ressort de constante de
raideur k.
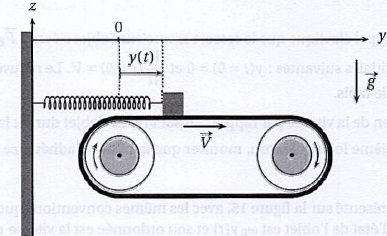
La position de l'objet, modélisé par un point matériel, est repérée par
son abscisse y(t). Lorsque l'objet se trouve en y=0, le ressort n'est
ni tendu, ni comprimé : sa longueur est égale à sa longueur à vide.
21. Portrait de phase de l'oscillateur
harmonique.
Dans les
questions 47 à 50, on fait l'hypothèse que le tapis est immobile et que
l'objet se déplace sans frottement sur le tapis.
Dans ces conditions : y(t) = y0 cos ( w0t).
47. w0 = ka mb où a et b
sont des réels. k s'exprime en N m-1. Quelle est l'unité de w0
? Déterminer a et b.
w0t étant sans
dimension, w0 est l'inverse d'un temps ( s-1).
k est une force divisée
par une longueur ; une force est une masse fois une accélération.
k s'exprime en : kg s-2. k / m s'exprime en s-2. (k / m)½ sexprime en s-1.
Donc a = 0,5 et b = -0,5.
48. Déterminer l'expression de la
vitesse de l'objet.
v(t) = dy / dt = -w0 y0
sin (w0t).
On convient de représenter l'état de l'objet par un point N dans un
plan muni d'un repère orthonormé. l'abscisse du point N est égale à w0 y(t) et son ordonnée à v(t). La courbe
décrite par ce point N lorsque le temps évolue est appelée portrait de
phase du système étudié.
49. Justifier quelle portrait
de phase est un cercle, centré sur l'origine et de rayon w0 y0. Indiquer le sens de
parcours et la position initiale de N.
abscisse x(t)= w0 y0
cos ( w0t)
; ordonnée v(t) = -w0 y0
sin (w0t).
x(t) 2 + v(t)2 = (w0 y0)2.
Il s'agit de l'équation d'un cercle centré sur l'origine et de rayon R =w0 y0.
Position initiale : abscisse : y0 ; ordonnée : 0.
Sens de parcours : celui des aiguilles d'une montre.
50.
Comment se traduit sur le portrait de phase le caractère périodique du
mouvement de l'objet ? Tonner l'expression de la période T0.
N décrit le cercle
en une durée T0 constante.
w0 T0 = 2 p. T0 =2 p / w0.
2.2. Portrait de phase de
l'objet entraîné par le tapis.
On considère que la partie supérieure du tapis se déplace par rapport
au sol à la vitesse V > 0. On tient compte de forces de frottements
qui s'exercent sur l'objet. L'actionn mécanique du tapis sur l'objet
est modélisée par une force 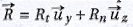 qui suit les lois de
Coulomb du frottement de glissement : qui suit les lois de
Coulomb du frottement de glissement :
- l'objet adhère au tapis tant que |Rt| < µs |Rn| où µs
est le coefficient de frottement statique.
- lorsque l'objet glisse sur le tapis, alors |Rt| = µd |Rn| où µd est le coefficient de
frottement dynamique.
La force de rappel élastique exercée par le ressort s'écrit : 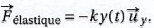
On choisit les conditions initiales suivantes : y(0)=0 et dy /dt ( t=0)
= V. Le mouvement de l'objet débute par une phase d'adhérence sur
le tapis.
51. Déterminer
l'expression de la vitesse par rapport au sol v(t) de l'objet
durant la phase d'adhérence.
L'objet adhérant au tapis possède la même vitesse que le tapis : v(t) =
V.
52. En appliquant
la seconde loi de Newton, montrer que la phase d'adhérence se maintient
tant que |y| < µs
mg / k.
On écrit la seconde loi de Newton sur l'axe horizontal. L'objet
ayant la vitesse constante du tapis V, son accélération est nulle.
Par suite : k y(t)= Rt.
Sur l'axe vertical, cette loi conduit à mg = Rn.
L'objet adhère au
tapis tant que |Rt| < µs |Rn| soit ky(t)
< mg µs.
Le portrait de phase est représenté ci-dessous. La phase de glissement
correspond à une portion de cercle, centré sur la point C de
coordonnées w0
µd mg / k ; 0). Le cercle complet est parcouru avec une
vitesse angulaire constante, en une durée T0 déterminée à la
question 50.
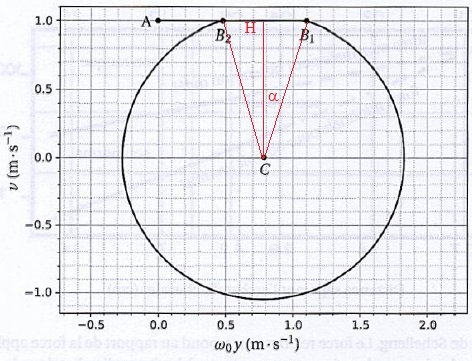
53. Donner la
valeur de la vitesse V.
La vitesse est constante ( adhérence) entre les points A et B1
et vaut V = 1,0 m /s.
54. Que représente
le point A ? A quelle partie du portrait de phase correspond la phase
d'adhérence ?
A est la position initiale de l'objet. AB1 correspond àla
phase d'adhérence.
55. Justifier que
le mouvement devient périodique, une fois B2 dépasé pour la
première fois. Décrire ce mouvement.
L'objet par du point A, à vitesse constante : l'abscisse y augmente. Il
dépasse le point B2 puis suit ce portrait sans jamais
repasser sur le segment AB2. Le mouvement est donc bien
périodique dès lors que B2 est dépassé pour la première fois.
Tant que la
vitesse est positive,
l'abscisse y croît. Quand la vitesse devient négative, y décroît : le
portrait de phase se décrit dans le sens des aiguilles d'une montre.
56. Donner les durées de la phase
d'adhérence, de la phase de glissement, la période du mouvement.
T0 est donnée égale à 1,0 s ; w0 = 2 p. V = 1,0 m /s.
Distance w0
B2 B1 =0,6 m /s
Ta = 0,6 / (6,28) ~0,09 s.
tan a = HB1
/ CH =0,3 / 1 =0,3 ; a
~17 °.
Portion du cercle correspondant au glissement : (360-2*17) / 360 ~0,91.
Durée du glissement Tg = 0,91 T0 = 0,91 s.
Période du mouvement : 0,91 +0,09 = 1 s.
57. En quoi ce
modèle est-il pertinent pour décrire l'action de l'archet sur la corde
? Quelles sont les granndeurs caractéristiques de la corde du violon
analogues à la masse m, à la constante de raideur k, à la vitesse V et
aux coefficients de frottement.
Ce modèle est pertinent car il décrit les phases d'adhérence et de
glissement qui se succèdent sur la corde du violon.
k ( N / m) correspond à la tension de la corde du violon divisée par la
distance ß L.
V correspond à la vitesse va de l'archet.
58. En quoi ce
modèle est-il criticable pour décrire le mouvement d'une corde de
violon frottée ?
Pour la corde de violon : la phase d'adhérence est longue, la
phase de glissement est courte. C'est le contraire du modèle décrit
ci-dessus.
De plus le modèle du tapis ne prend pas en compte la présence
d'harmoniques.
|
|

 Mouvement de la table d'harmonie.
Mouvement de la table d'harmonie.





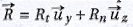 qui suit les lois de
Coulomb du frottement de glissement :
qui suit les lois de
Coulomb du frottement de glissement :