dipole RL cours exercices
dipole RC En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. .. .. fiche cours . .
une bobine inductive est un réservoir d'énergie	constante de temps = L / R elle donne l'ordre de grandeur de la durée du régime transitoire, lors de l'ouverture ou de la fermeture d'un circuit.
tension aux bornes de la bobine L inductance (H) r resistance (W) si l'intensité est constante, la bobine se comporte comme un conducteur ohmique
énergie stokée 0,5 L i2
exercice 1 constante de temps dans un dipole (RL) Aux bornes d'un générateur de tension continue de 6 V, on branche une bobine d'inductance L=11 mH, de résistance r =1 ohm en série avec un conducteur ohmique de résistance R=1kW. La constante de temps t caractéristique de l'établissement du courant est : 6,6 ms ; 11 ms ; 1,1 10-6 s ; 11ms ; 66 ms. corrigé Le retard à l'établissement du courant est voisin de 5 fois la constante de temps. la constante de temps est : inductance divisée par la somme des résistances 0,011 /1001=1,1 10-5 s soit 11 ms 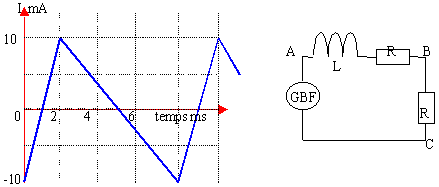retour - menu exercice 2 auto induction données L=0,3 H et r=0 R=50 W La bobine traversée par un courant variable d'intensité i est le siège de phénomène d'auto induction . La tension à ses bornes est Entre 0 et 2 ms l'intensité est égale à i(t)=5t-10 et entre 2 et 5 ms i(t)= -5t+constante (20 mA) La tension aux bornes de la bobine varie entre -3 et +1 V L'énergie électromagnétique emmagasinée dans la bobine a pour valeur maximale 0,015 mJ. corrigé la première affirmation est vraie faux calculer le coefficient directeur des deux segments de droites [0;2] fonction croissante de coef. directeur 0,02 (A) divisé par 0,002 (s)=10As-1 [2;8] fonction décroissante de coef. directeur0,02 (A) divisé par 0,006 (s)= -3,33As-1 cette affirmation est vraie il suffit de multiplier L par l'un puis l'autre coéf. directeur trouvés ci dessus. 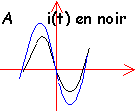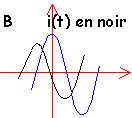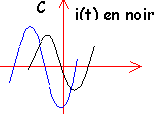0,3*10= 3 V et 0,3* -3,33 =-1 V vrai la bobine est un réservoir d'énergie ; l'énergie maximale stockée est 0,5 L i2 avec i maxi =0,01 A 0,5*0,3*0,012=0,15 10-4 J =0,015 mJ exercice 3 nature d'un dipole Un dipole est parcouru par un courant sinusoidale i(t). On visualise à l'oscilloscope l'intensité et la tension à ses bornes. Quel est sa nature dans les 3 cas ci dessous ? corrigé A: intensité et tension en phase: résistor RLC à la résonance d'intensité B: intensité en avance de p/2 sur la tension condensateur C: intensité en retard de p/2 sur la tension bobine inductive retour - menu exercice 4 dipole RL L'intensité passe d'une valeur égale à 10% de sa valeur maximale à une valeur égale à 90% de sa valeur maximale, sur une durée Dt=2,2 t (t=L/R), constante de temps du circuit A l'aide du graphique en déduire t.  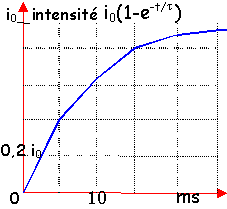 corrigé tracer 2 droites horizontales passant par 0,1 i0 et 0,9 i0 A partir des 2 intersections avec la courbe , tracer 2 verticales. déterminer sur le graphe la distance séparant ces 2 verticales; tenir compte de l'échelle; cet intervalle de temps vaut 2,2 t t voisin de 10 ms ou bien à t=t l'intensité vaut 63% de sa valeur finale. retour - menu