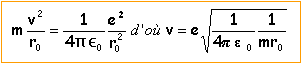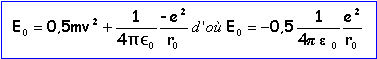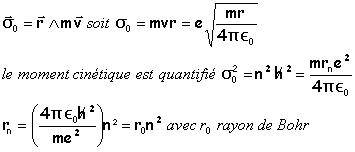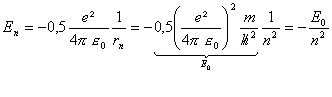|
|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
relation de Balmer: à la fin du XIX e siècle il établit une formule donnant la longueur d'onde des raies du spectre de l'atome d'hyrogène  postulats de Bohr: l'atome d'hydrogène peut être représenté comme un système planétaire dans lequel l'électron occupe des orbites stables sur lesquelles il ne rayonne aucune énergie. A chaque orbite de l'électron correspond un niveau d'énergie de l'atome. L'électron passe d'une orbite à une autre soit en émettant un photon (retour - menu à un état plus stable de moindre énergie) soit en absorbant un photon (l'atome se trouve alors dans un état excité) Dans les 2 cas l'énergie du photon est: hn=En-Em où h est la constante de Planck 6,26 10-34 Js; n: fréquence en Hertz; En-Em différence d'énergie entre 2 niveaux. Sommerfeld complète le modèle de Bohr en remplaçant les orbites circulaires par des orbites elliptiques. 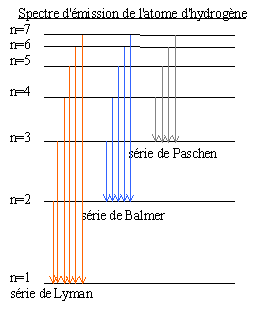
|
|
|
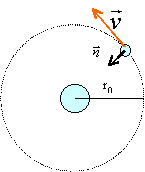
trajectoire de l'électron, énergie |
1 / (4 p e0)=9 109 SI On considère le modèle de Bohr de l'atome d'hydrogène. Le proton supposé fixe est l'origine O d'un référentiel galiléen. Le poids de l'électron est négligeable devant la force attractive de Coulomb.
|
|
|
|
relation fondamentale de la dynamique projetée suivant le vecteur n
aspect énergétique
|
|
|
moment cinétique quantifié |
|
|
|
|
moment cinétique de l'électron par rapport au noyau
l'énergie mécanique de l'électron devient quantifiée:
E0 représente l'énergie mécanique de l'électron dans l'état fondamental. r0= 5,33 10-11 m; E0 = 2,18 10-18 J =13,6 eV |