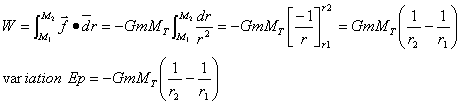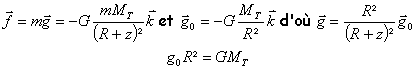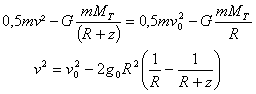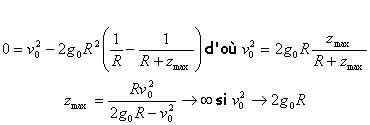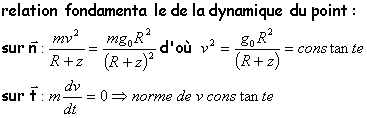gravitation

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

1

travail de la force de gravitation
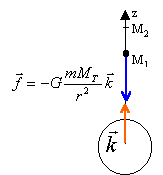
Un corps M de masse m est lancé depuis la surface de la terre verticalement vers le haut avec une vitesse initiale v0. Son mouvement est rectiligne et sa position est repérée sur un axe vertical vers le haut, l'origine étant le centre de la terre.

Montrer que le travail de la force de gravitation est l'opposée de la variation d'énergie potentielle Ep=-G mMT / r. (r : distance de M au centre de la terre).

corrigé


Au cours du déplacement M1M2, travail de la force gravitationnelle.

2

vitesse à

l'altitude z
 

 

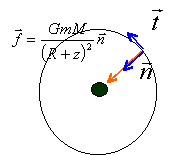
Donnez l'expression du champ de gravitation en faisant apparaître la valeur g0 , champ au niveau du sol; en déduire la relation liant GMT et g0R² (R :rayon terrestre).

Exprimer la vitesse du corps à l'altitude z. R=6370 km ; g0 =9,81 m/s².

corrigé


champ de pesanteur à l'altitude z

La force de gravitation est conservative, l'énergie mécanique du corps se conserve au cours du mouvement.
3

vitesse de libération
Déterminer la vitesse de libération (vitesse minimale de lancement pour que le corps ne retombe pas sur terre). Quelle est son énergie mécanique ?
corrigé


Si la vitesse de départ n'est pas suffisante, le corps atteint l'altitude zmax puis retombe.

application numérique : v0 = 11,2 km/s

l'énergie mécanique est positive ou nulle , ce qui caractérise un corps pouvant s'échapper de l'attraction terrestre.
4

satellite circulaire
 

 Montrer de 3 façons différentes que son mouvement est uniforme.

Exprimer la vitesse et la période..

corrigé


système : le satellite

référentiel géocentrique considéré galiléen

le satellite n'est soumis qu'à la force de gravitation

La force de gravitation est perpendiculaire à la vitesse : donc elle ne modifie pas l'énergie cinétique. La norme de la vitesse est constante.

Le satellite décrit la circonférence à la vitesse v pendant une période T:
5

satellite géostationnaire
 

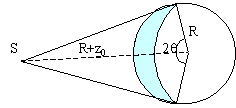
Quelle est sa période ? Dans quel plan est-il situé ? A quelle altitude évolue t-il ?

Quelle fraction de la surface de la terre peut être couverte par les émissions du satellite?

On donne la surface d'une calotte sphérique d'une sphère de rayon R vue sous un angle 2q. S=2pR²(1-cosq)

corrigé


Le satellite géostationnaire paraît immobile pour un observateur terrestre. Sa trajectoire circulaire est dans le plan de l'équateur. Sa période est égale à la période de rotation de la terre dans le référentiel géocentrique.

T0=86 164 s. Son altitude est voisine de 36 000 km

surface de la terre : 4pR²

surface couverte par le satellite : 2pR²(1-cosq) avec cosq = R / (R+z0)

fraction de la surface :0,5(1-cosq) = 0,5(1-R / (R+z0))

environ 42%

6

altitude faible devant le rayon R
Faire un développement limité au premier ordre des expressions de la vitesse et de la période à une altitude z<<R

Calculer v et T pour z=0,200,400,600 km

corrigé


z (km)
0
200
400
600
vitesse (m/s)
7900
7780
7670
7860
période (s)
5060
5300
5500
5700

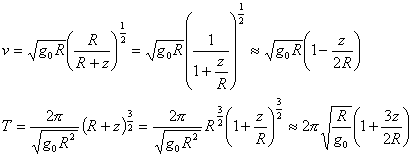
retour - menu