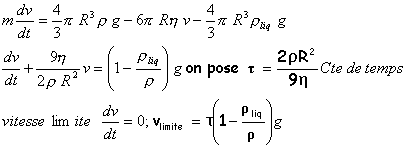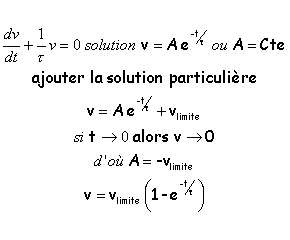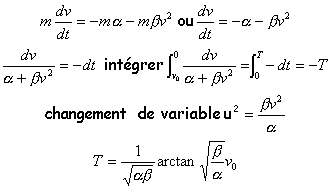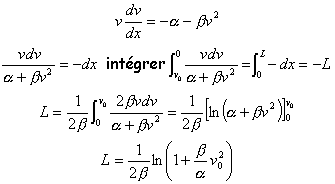frottements

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.


1

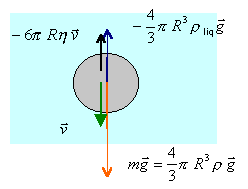
chute dans un milieu visqueux
La sphère de rayon R, de masse volumique r est lachée sans vitesse dans un liquide de masse volumique rliq, de viscosité h. La sphère est soumise à son poids, à une force de frottement visqueux et à la poussée d'Archimède.

Ecrire l'équation différentielle à laquelle obéit la vitesse, l'intégrer puis calculer la vitesse limite de chute.

R=0,1 cm; r =7,9 g cm-3; rliq= 1 g cm-3;h=14g cm-1 s-1.

corrigé


système : sphère ; référentiel terrestre galiléen

projection de la relation fondamentale de la dynamique du point sur un axe vertical orienté vers le bas

L'équation différentielle est du premier ordre à coefficients constants avec un second membre. La solution est la somme de la solution générale de l'équation sans second membre et d'une solution particulière de l'équation avec second membre ( la vitesse limite est cette solution particulière).
2

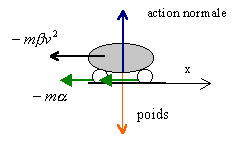
freinage d'une auto- durée du parcours
 

 

La voiture est soumise à une force de frottement solide ma et à la résistance de l'air mbv² où v est la vitesse et a b des constantes.Le conducteur arrête le moteur, la vitesse étant v0.

Déterminer l'équation différentielle permettant de trouver la vitesse.

Quelle est la durée du parcours avant l'arrêt de l'auto ?

corrigé


système : voiture ; référentiel terrestre galiléen

projection de la relation fondamentale de la dynamique sur un axe horizontal orienté vers la droite
3

freinage d'une auto-distance d'arrêt
 

Etablir l'équation différentielle liant les variables x et v puis exprimer la distance parcourue moteur coupé.

corrigé


On élimine la variable temps en écrivant que v=dx / dt ou dt = dx/ v

retour - menu