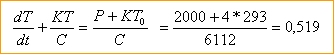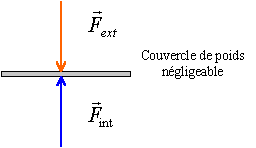autocuiseur

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .
.
.

1

durée du chauffage
T0=20°C; P0=1,013 bar; Ceau=4180 J K-1 kg-1.

le récipient : D=28 cm; h=16 cm ; m=4,2 kg ; c=460J K-1 kg-1.

puissance du système de chauffe : 2 kW

 

  1. A la date t=0 on place 1 L d'eau prise à 20 °C dans l'autocuiseur. On suppose que l'air surmontant le liquide est sec, pas de formation de vapeur.On néglige les pertes thermiques vers l'extérieur. Quelle est la durée du chauffage pour atteindre 100 °C (sans ébullition de l'eau).
  2. On tient compte des pertes par convection entre le récipient et l'extérieur. La puissance perdue P' est proportionnelle à l'écart de température P'=4 DT.Quel est la nouvelle durée du chauffage ?
  3. Est-il réaliste de négliger la présence de la vapeur d'eau avant que l'on atteigne 100 °C ? (vapeur à 100 °C sous 1,013 bar :0,6 kgm-3. chaleur latente de vaporisation 2 257 kJ kg-1)
corrigé


les capacités thermiques du récipient et de l'eau s'ajoutent :

C=1*4180+4,2*460 = 6112 J K-1.

puis multiplier par l'écart de température 100-20 =80° pour obtenir l'énergie :

488 960 J

diviser par la puissance (en watt) pour obtenir la durée du chauffage :

488 960 / 2000 = 244 s =4 min 4 s

Bilan énergétique entre les instants t et t+ dt, la température passe de T à T+dT

dQ= C dT + K(T-T0) dt

La puissance fournie par le système sert à élever la température et à compenser les pertes.

P = dQ/dt = CdT/dt + K(T-T0)

Tfinale =293 K ; d'où t=226 s = 4 min 26 s.

volume du récipient : pr²h= 9,85 L

volume de la vapeur 9,85- volume de l'eau =8,85 L

masse de vapeur : 8,85 10-3 * 0,6 = 5,3 g

chaleur nécessaire au changement d'état : 5,310-3 *2 257 =12 kJ

quantité négligeable devant 489 kJ.
2

étude du régime permanent
 

La pression à l'intérieur du récipient a atteint la valeur de régime soit 1,69 bar et la tempèrature est de 115 °C. L'air a été entierement chassé, la vapeur d'eau est en équilibre avec le liquide. On continue à chauffer et la soupape se met en rotation : un jet est éjecté. Dans ces conditions (vapeur 0,965 kgm-3. chaleur latente de vaporisation 2 215 kJ kg-1)

  1. Quelle masse de vapeur surmonte le liquide ? (masse d'eau voisine de 1kg)
  2. Quel est le débit de l'eau qui s'échappe par la soupape ?
  3. Quel est l'état physique (liquide, vapeur) du jet qui s'échappe et quelle est sa température ?
corrigé


volume de la vapeur :8,85 L

masse de vapeur : 8,85 10-3 *0,965 = 8,54 g

La puissance fournie sert à évaporer l'eau et à compenser les pertes.

pertes par convection à 115 °c : 4(115-20)=380 W

puissance utile à évaporer l'eau : 2000-380=1620 W

1620 = 2,215 106 * débit massique (kg s-1)

débit = 7,31 10-4 kg s-1=0,731 g s-1.

Le jet est une détente brutale sans échange de chaleur avec l'extérieur (adiabatique).

La vapeur se refroidit brutalement et le jet est formé de fines gouttes d'eau à la température de 100°C sous 1,013 bar.
3

arrêt du chauffage
 

On arrête le chauffage. La soupape se referme dés que la pression est inférieure à 1,69 bar. On laisse le récipient et son contenu revenir à la température ambiante.( à 20 °C la pression interne est 0,0234 bar).

  1. Pourquoi le couvercle semble coller au récipient ?
  2. Quelle force faudrait-il exercer sur le couvercle pour le décoller ?
  3. Comment faire pour l'ouvrir simplement ?
corrigé


à 20 °C la pression interne est inférieure à la pression extérieure. Cette grande différence de pression colle le couvercle sur le récipient.

à l'équilibre les deux forces se neutralisent .

Pour rompre cet équilibre il faut exercer la force :

Force = (Pext-Pint) * surface du couvercle

pression en pascal et surface en m²

F = (1,013-0,0234)105*3,14*0.14²= 6100 N

il vaut mieux enlever la soupape (sa section étant faible c'est facile) et laisser les pressions s'égaliser avant de retirer le couvercle.

retour - menu