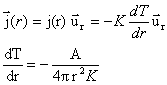Aurélie sept 2001
Equilibre thermique d'un mamifère

Capes interne 96

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

Un mamifère peut être sommairement schématisé par une sphère de muscle de centre O et de rayon R dont le métabolisme dégage une quantité de chaleur P par unité de volume et de temps.

Un point N de l'espace est repèré par sa distance à O, notée ON=r. L'animal est plongé dans de l'eau ou dans de l'air, c'est à dire que pour r>R, il y a un matériau de conductivité thermique K; la température à l'infini est la température ambiante et vaut T0 =20°C.

La situation décrite est à symétrie sphérique et est décrite par :

- la partie interne (r <R) qui produit une quantité de chaleur P par m3 et par seconde.

- pour r >R: milieu ambiant de conductivité thermique K ; la température pour r infini vaut T0=20°C.

On va s'intéresser aux phénomènes de transport de chaleur en régime permanent, c'est à dire indépendant du temps. On rappelle la définition du vecteur densité de courant de chaleur : la quantité de chaleur qui traverse une surface élémentairedS(N) pendant dt est donnée par la relation :

 

où est le vecteur densité de courant de chaleur en N.

On rappelle la loi de Fourier concernant la diffusion de la chaleur.

 

Dans tout le problème l'espace sera repèré par un repère sphérique de centre O. On rappelle l'expression du gradient en coordonnées sphériques.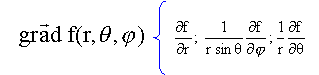

 
  1. Quelle est la signification physique du signe moins dans la loi de Fourier?
  2.  Déterminer la direction du vecteur en tous points de l'espace.
  3. De quelles variables d'espace dépend le vecteur ?
  4. déterminer la quantité de chaleur dégagée par unité de temps par l'animal en fonction de P et R.
  5. Exprimer le vecteur aux points r=R.
  6. Montrer que pour les points tels que r supérieur ou égal à R, alors , ou A est une constante indépendante de r; on notera j(N) la norme du vecteur . Exprimer A.
  7. Déterminer l'équation différentielle vérifiée par la température T(r) pour r supérieur ou égal à R.
  8. Déduire des questions précédentes l'expression de la température en fonction de r, T0, R, K et P.
  9. Quelle est la température cutanée de l'animal Tc en r = R.
  10. Quelles doivent être les valeurs de P pour que Tc=30°C. dans l'eau puis dans l'air. On donne pour l'eau K= 500 J m-1s-1; pour l'air K= 5J m-1s-1.R=25 cm ( ces valeurs permettent d'avoir un rapport surface sur volume voisin de celui de l'être humain).
  11. Pourquoi n'existe-t-il pas de petits mamifères marins?

corrigé

Le vecteur densité de courant de chaleur possède le sens des températures décroissantes, d'où le signe moins dans la loi de Fourier.

Le centre O est centre de symétrie pour le système

le vecteur doit refléter cette symétrie; ce dernier ne dépend que de r.

Quantité de chaleur dégagée par l'animal par unité de temps:

V= 4/3 pR3, volume de la sphère de rayon R

en prenant comme surface d'intégration une sphère de rayon R, on obtient :

et en identifiant avec le résultat de la question précédente :

j(R) =R/3 P

On considère une sphère de rayon r >R :

en régime stationnaire ce flux de chaleur est constant et est égal à A

équation différentielle: utiliser la loi de Fourier, le gradient n'a qu'une composante suivant r

intégration de cette expression :

pour déterminer la constante d'intégration, il suffit d'écrire que lorsque r tens vers l'infini la température est égale à T0=20°C

puis remplacer A par son expression

température cutanée de l'animal :

pour r=R, T=Tc soit : Tc= R²P / (3K) + T0.

P = 3K / R² (Tc-T0)

dans l'eau : P= 240 kWm-3 et dans l'air : P= 2,4 kWm-3.

Dans l'eau pour maintenir un organisme à température constante la puissance thermique mise en jeu est 100 fois plus importante que dans l'air.

Cette puissance est inversement proportionnelle au carré de R: seuls les gros mamiféres seront capables de produire une énergie thermique suffisante au maintien d'un température cutanée fixée.

retour - menu