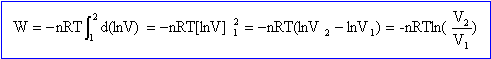|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
| .
. |
|
|
|
|
|
|
|
à n et T constante p1v1 = p2v2 d'où v2 = v1 p1 / p2 = 10 m3. travail élémentaire des forces de pression -pdV= -nRT /V dV = -nRT d(lnV) intégrer entre v1 et v2.
avec nRT=p1v1 = p2v2 et p1= 106 Pa ; v1 = 1 m3 ; v2 /v1 = 10 W = -106 ln 10 = -2,3 106 J L'énergie interne d'un gaz parfait de dépend que de la température ; si T=cte alors DU=0 or DU= W+Q donc Q= -W=
2,3
106
J
p1V1g = p2V2g s'écrit (V2/V1)g = p1 /p2 = 0,333 avec g = 5/3 V2/V1 = 0,3333 (3/5) = 0,517 V2 = 5,17 L. travail élémentaire des forces de pression -pdV avec p= Cte / Vg intégrer entre V1 et V2.
pression en pascal, volume en m3. W = (3 105 * 5,17 10-3 - 105*10-2) / (1,666-1) = 2125 J. adiabatique donc Q= 0 DU = W+Q = W DU = nR D T avec n = 2 / masse molaire hélium = 2/4 = 0,5 D T =2125/(0,5*8,32) =
511
K.
D U= W + Q absorbe 2000 J donc Q= +2000J fournit un travail donc W = - 500J D U= +1500 J. volume constant donc pas de travail des forces de pression W = 0 cède donc Q= -5000 J D U= -5000 J. adiabatique donc Q = 0 et W= 80 J D U= +80 J. changement d'état à pression et température constante Q= +L = 2,26 106 J W= -P D V = -105 (1,671 -10-3 ) = -1,67 105 J D U= +2,09 106 J.
retour - menu |