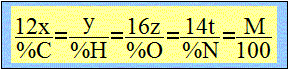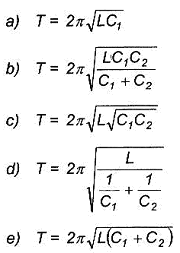Analyse détaillée d'exercices réalisés sous forme de QCM.   En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

aspartame. Texte :A la date t=0 on branche aux bornes d'un dipôle RL un condensateur de capacité C chargé sous une tension E. Il se produit des oscillations pseudo-périodiques dans le circuit. Que représente la pseudo-période des oscillations ? La durée séparant deux dates successives où la tension aux bornes du condensateur est maximale et de même valeur. Vrai. La durée au bout de laquelle le condensateur a perdu 63 % de sa charge initiale. Faux La durée séparant deux dates successives où la tension aux bornes du condensateur est nulle. Faux L'intervalle de temps séparant deux dates successives où l'énergie emmagasinée dans la bobine est maximale .Faux L'intervalle de temps séparant deux dates successives où l'intensité du courant dans le circuit est maximale. Faux Analyse : Question relative à la formule brute de l'aspartame. On note CxHyOzNt la formule brute de l'aspartame et M sa masse molaire. x, y, z, t, nombres entiers positis. Exprimer la masse d'eau en mole : m/M =1,62 / 18 = 0,09 mol d'eau à partir de 0,01 mol d'aspartame. CxHyOzNt + .... O2 conduit à ....... + ½y H2O. 0,01 mol.............................................0,09 mol 1 mol............................................. 9 mol soit y = 18.   Chercher des relations entre x, y, z et t : 12 x / 57,14 = y / 6,12 ; 0,21 x = 0,163 y ; x = 0,163/0,21 y x = 0,163/0,21*18 ; x=14. y / 6,12 = 16z/ 27,22 ; 0,163 y = 0,588 z z = 0,163*18/0,588 ; z = 5.   y / 6,12 =14t / 9,52 ; 0,163 y = 1,47 t ; t = 0,163*18 / 1,47 ; t = 2. C14H18O5N2   Electrolyse. Texte : Un dipôle (L, C1) constitué d'une bobine d'inductance L, de résistance interne négligeable, et un condensateur de capacité C1 est branchée en série aux bornes d'un condensateur de capacité C2 préalablement chargé. On observe des oscillations sinusoïdales libres. Quelles sont les expressions littérales possibles pour la période T de ces oscillations ? Deux condensateurs en série sont équivalents à un condensateur unique de capacité C=C1C2/(C1+C2). La période est du type T=2p (LC)½ d'où b) et d) Analyse : Question relative au dégagement gazeux. A l'anode une oxydation se produit. Au regard des couples oxydant / réducteur en présence, seule l'eau peut s'oxyder en dioxygène suivant : H2O = ½O2 + 2H+ + 2e-. La quantité de matière (mol) de dioxygène est donc 4 fois plus faible que la quantité de matière d'électrons n(O2 )= 0,25 n(e-). (1) Question relative à la quantité de matière d'électron. Quantité d'électricité Q= I Dt. Dt = 2*3600 + 35*60 =9300 s. Q = 1,5*9300 = 13950 C Or Q = 96 500 n(e-) ; n(e-) = 13950/96500 =0,1445 mol. Question relative au volume de gaz. (1) donne n(O2) = 0,25*0,1445 = 0,0361 mol V = n(O2) *Vm = 0,0361*25 =0,90 L.     Web www.chimix.com Oxydoréduction. Texte : Un circuit oscillant de type LC, utilisé dans un récepteur radio, est formé d'une bobine d'inductance L = 0,50 m H et d'un condensateur de capacité C. La fréquence propre de ce circuit vaut f0 = 10 MHz. Quelle est la valeur de la capacité C ? a) 0,5 nF b) 2 nF c) 5 nF d) 10 nF e) 20 nF L= 5 10-7 H ; f0 = 107 Hz ; w= 2p 107 rad/s ; à la résonance : LCw²=1 soit C= 1/(Lw²)= 1 / (5 10-7*(2p 107 )²)=10-7 / 200 = 10-9/2 = 0,5 nF réponse a : correcte Analyse : Question relative à l'équation de la réaction. La concentration finale en ion fer (II) est inférieure à la concentration initiale , le volume de la solution restant constant. Donc l'ion fer (III), l'oxydant, s'est réduit en ion fer (II) suivant : Fe3+ aq + e- = Fe2+ aq. Le métal argent constitue le réducteur : il va s'oxyder en ion Ag+ : Ag = Ag+aq+ e-. Par suite : Fe3+ aq +Ag = Fe2+ aq + Ag+aq. La masse d'argent diminue. Question relative à la constante de la réaction. K = [ Fe2+]éq [Ag+]éq / [Fe3+]éq ; avancement volumique (mol/L) Fe3+ aq +Ag = Fe2+ aq + Ag+aq. départ 0 0,01 excès 0 0 équilibre xéq 0,01-xéq = 3,0.10-4 xéq =9,7.10-3 xéq =9,7.10-3 K = 9,7.10-3 * 9,7.10-3 / 3,0.10-4 = 0,31. Question relative au quotient initial. Qr i = [ Fe2+]i [Ag+]i / [Fe3+]i ; Or [ Fe2+]i = [Ag+]i=0 donc Qr i =0. Le quotient de réaction initial est inférieur à K. Un condensateur de capacité C= 5mF est chargé sous une tension constante U=12 V. Il est ensuite branché aux bornes d'une bobine d'inductance L et de résistance interne négligeable. On constate que la valeur maximale du courant qui circule dans le circuit est 200 mA. - Quelle est la valeur de l'inductance de la bobine ? (0,3 mH ; 18 mH ; 30 mH ; 0,6 H ; 1 H) énergie stockée par le condensateur : ½CU² = 0,5*5 10-6 * 12² = 3,6 10-4 J. échange d'énergie entre bobine et condensateur : la bobine peut stockée au maximum ½LI²max d'où L= 2* 3,6 10-4 / 0,2² = 0,018 H = 18 mH. Un circuit RLC série est alimenté par une tension sinuso<îdale de fréquence réglable, de valeur efficace U ; l'inrensité efficace est notée I et l'impédance est notée Z. Pour la fréquence f0, le circuit est dit résonant. L'intensité efficace à la résonance est notée I0. Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ? Pour une fréquence quelconque, la puissance consommée est P= RI2. Pour une fréquence quelconque, la puissance consommée est P= R(U/Z)2. Pour une fréquence f0, la puissance consommée est P= RI02. La puissance consommée est minimale quand Z= R. La puissance consommée par le condensateur est nulle.  corrigé Pour une fréquence quelconque, la puissance consommée est P= RI2. 1 est vrai. or I= U/Z d'où P= R(U/Z)2. 2 est vrai. Pour une fréquence f0, la puissance consommée est P= RI02. 3 est vrai. L'intensité étant maximale à la résonance, la puissance consommée est alors maximale. 4 est faux. La puissance moyenne consommée par le condensateur est nulle. 5 est vrai.

retour -menu