dipôle RL. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

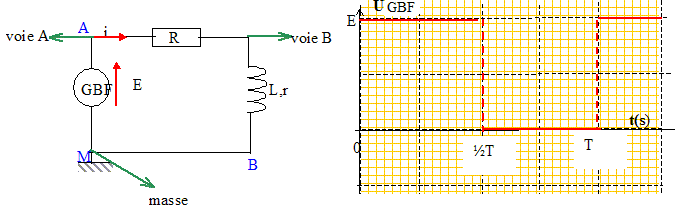
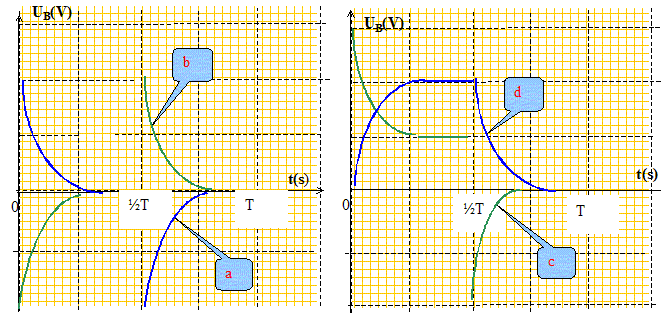
Etude de courbes. Texte : on associe en série une résistance R=200 W et d'une bobine ( L=10 mH ; r = 100 W ). Le générateur basse fréquence ( GBF) délivre une tension crénaux de fréquence f = 500 Hz. Analyse : Question relative à l'allure du signal voie B. Sur la voie B on observe la tension aux bornes de la bobine inductive : u= Ldi/dt + ri. Sur l'intervalle [0 ; ½T = 10-3 s] : A l'instant initial i=0 : u = Ldi/dt. La constante de temps de ce dipole RL est t = L/(R+r) = 0,01 / 300 = 3,3 10-5 s. La période de la tension délivrée par le GBF est : 1/500 = 2 10-3 s. En conséquence on atteint très rapidement le régime permanent et di/dt = 0 soit u=rI avec I = E/(R+r). La tension aux bornes de la bobine décroît de la valeur Ldi/dt à la valeur rI.   Sur l'intervalle [10-3 ; 2 10-3 s] : di/dt est négatif ( décroissance de l'intensité) et l'intensité initiale n'est pas nulle. Le terme Ldi/dt l'emporte sur ri et la tension aux bornes de la bobine est négative. En régime permanent, la tension aux bornes du GBF est nulle ; la tension aux bornes de la bobine est nulle. La tension aux bornes de la bobine croît à partir d'une valeur négative jusqu'à la valeur zéro. La courbe représentant la tension aux bornes de la bobine présente une discontinuité : ( d est à exclure)   Durant la première demi-période la tension aux bornes de la bobine en régime permanent n'est pas nulle :( a et b sont à exclure) Donc choix de la courbe c.   Intensité du courant. Texte : Interrupteur étant en position 1 le régime permanent s'établit ; l'interrupteur est basculé en position 2. L'origine des temps est la date du basculement rapide. Analyse : Question relative à l'expression de l'intensité. Solution de l'équation différenteille du type i (t)= A exp(-t/t) avec t = L/(R+r). La conservation de l'énergie entraîne la continuité de l'intensité. La valeur de l'intensité à t=0 est égale à valeur de l'intensité en régime permanent lorsque l'interrupteur était en position 1 : i0= E/(R+r) à 0. D'où A = E/(R+r) et i(t) =E/(R+r)exp(-t/t).     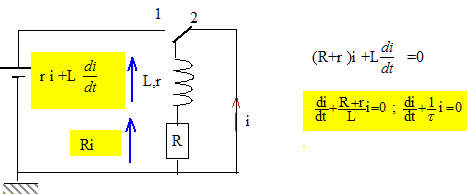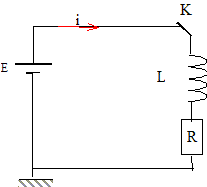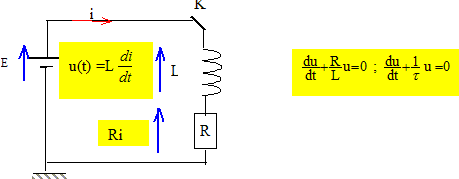Web www.chimix.com tension aux bornes de la bobine. Texte : On note u(t) la tension aux bornes de la bobine. A la date t=0, on ferme l'interrupteur. Analyse : Question relative à l'expression de u(t). additivité des tensions : E = u(t) + Ri (1) avec u(t ) = L di/dt soit di/dt = u(t) / L dériver (1) par rapport au temps : 0 = du/dt + R di/dt ; 0 = du/dt + R/L u(t). On pose t= L/R solution de cette équation différentielle u(t) = A exp(-t/t). A t=0, l'intensité du courant est nulle : la tension aux bornes du résistor est nulle ; la tension aux bornes de la bobine est égale à E d'où A = E et u(t) = E exp(-t/t). En régime permanent la tension aux bornes de la bobine est nulle.

retour -menu