Oscillateur élastique ( ressort). En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

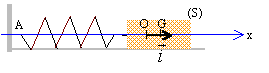
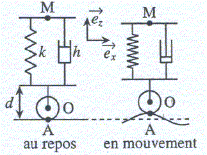
Oscillateur horizontal. Texte : Ressort de masse négligeable, de raideur k. Les frottements sont négligés. Le ressort est comprimé d'une longueur A puis on le libère sans vitesse initiale. masse du solide période raideur oscillateur n°1 m1 T1 k oscillateur n°2 m2 T2 = 1,5 T1 k Analyse : Question relative à la relation entre m1 et m2. Expression de la période : T = 2p[m/k]½. T2 = 4p2 m/k ; à raideur k identique, le carré de la période est proportionnel à la masse. Si la période est multipliée par 1,5, T2 est multiplié par 1,52 = 2,25 ; m2 = 2,25 m1. Question relative à l'énergie cinétique maximale. Initialement, l'énergie mécanique est sous forme d'énergie potentielle élastique ½kA2. Au passage à la position d'équilibre, l'énergie mécanique est sous forme cinétique : ½m vmax2. Conservation de l'énergie mécanique : donc l'énergie cinétique maximale est égale à l'énergie potentielle élastique maximale soit ½kA2. Les conditions initiales étant identiques, l'énergie cinétique maximale reste constante.   Question relative à la vitesse maximale. ½m1 v1 max2 = ½m2 v2 max2 et m2 = 2,25 m1. m1 v1 max2 =2,25 m1 v2 max2 ; v1 max2 =2,25 v2 max2 ; v1 max=1,5 v2 max.   suspension d'un véhicule. Texte : Un véhicule automobile est modélisé par une masse m placée en M et reposant sur une roue de centre O par l'intermédiaire d'un ressort de raideur k mis en parallèle sur un amortisseur de coefficient de frottement h. Le véhicule roule sur une route comportant une succession régulière de bosses distantes de L ; pour une certaine valeur de la vitesse V du véhicule, il subit des oscillations verticales de forte amplitude. Analyse : Question relative à la vitesse V du véhicule. résonateur de période propre T0 = 2p(m/k)½ ; fréquence propre f0 = 1/T0 = 1/( 2p (k/m)½) excitateur ( la route ) : fréquence f = V/L à la résonance f= f0 soit : V/L = 1/( 2p (k/m)½) V= L/( 2p (k/m)½).     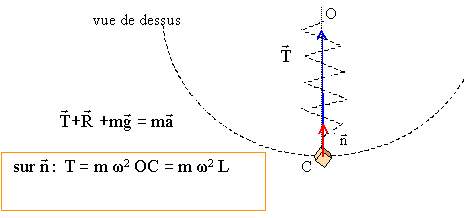Web www.chimix.com Rotation d'un ressort dans un plan horizontal. Texte : le ressort : raideur k, longueur à vide L0, masse négligeable, extrémité fixe O. A l'autre extrémité du ressort est accroché un solide de masse m. Le système {ressort + masse} tourne à vitesse angulaire constante w dans un plan horizontal ; le solide décrit une trajectoire circulaire de centre O. Analyse : Question relative à la longueur du ressort.   Or T= k( L-L0) ; par suite : k( L-L0) = mw2L L( k-mw2) = kL0 ; L = kL0 / (k-mw2).

retour -menu