|
Concours Esiee : 4 années de QCM Mouvement uniformément varié : plan incliné, mouvement circulaire, cinématique |
||||||||
|
||||||||
|
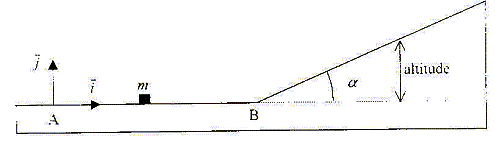
v0 = 4 m/s ; m = 100 g ; d= 7 m ; F=0,05 N; g = 10 m/s² ; sin a =0,1.
A- m arrive en B avec une vitesse de 3 m/s. Vrai. Th. de l'énergie cinétique entre A et B . m est soumise à son poids, à l'action du support et à la force de frottement : le poids et l'action du plan, perpendiculaires à la vitesse ne travaillent pas. Travail résistant des frottements W = -F AB = -F d = -0,05*7 = -0,35 J. DEc = ½mvB2 - ½mv02 = -0,35 ; vB2 = v02 - 2*0,35 / m ; vB2 =16-0,7/0,1 = 9 ; vB= 3 m/s. B- m parcourt AB en 1,75 s. Faux. Ecrire la seconde loi de Newton selon i : -F = m a ; a = -F/m = -0,05/0,1 = -0,5 m/s². vitesse v(t) = at + v0 ; v(t) =-0,5 t + 4 ; tB =( 4-vB) / 0,5 ; tB = 2 s. C- m atteint l'altitude maximale 8 s après son lancement. Faux. Sur le plan incliné, m est soumise à son poids, à l'action du plan perpendiculaire au plan et au frottements. Ecrire la seconde loi de Newton selon un axe parallèle au plan dirigé vers le haut du plan : -mg sin a - F = ma ; a = -( g sin a + F/m) = -(10*0,1+0,05/0,1) ; a = - 1,5 m/s². vitesse v(t) = at+vB ; v(t) = -1,5 t +3 A l'altitude maximum il y a arrêt ( vitesse nulle) d'où t arrêt = 2 s. Durée totale du parcourt : 4 s.
( origines : le passage en
B) : distance parcourue sur le plan z(t) =
½at2 + vB t ;
z = 0,5(-1,5)
22+3*2 = 3 m. altitude atteinte =
distance parcourue * sin a
= 3*0,1 = 0,3 m =
30
cm. E- 4 s après son
lancement, la vitesse de m est
2m/s.
Faux. La durée totale du
parcours avant arrêt est de 4
s.
Max et Léon se rendent chez Jules en métro. Jules habite entre les stations S1 et S2 distantes de 1 km, plus précisément à 550 m de S1. Max et Léon empruntent la même rame de métro mais Max descend à la station S1 et Léon à la station suivante S2. Entre chaque station, le métro démarre avec une accélération g=1 m/s² jusqu'à atteindre la vitesse de 36 km/h qu'il garde pendant un certain temps, puis il décèlère avec g '= -1 m/s² jusqu'à l'arrêt. Dès que Max et Léon sortent du métro, ils marchent à la vitesse constante de 6 km/h A- Le métro parcourt la
distance S1S2 en 1 min 50
s.vrai
Une colonne de randonneurs avance en ligne droite avec une vitesse constante de 7,2 km/h. Jules, le randonneur de tête, se trouve constamment à 100 m de Léon, le randonneur fermant la marche. Max doit porter une bouteille d'eau à Jules de la part de Léon. Il court à une vitesse constante vMax le long de la colonne en mouvement. Lorsqu'il a remis la bouteille à Jules, il repart immédiatement vers Léon, toujours à la même vitesse vMax . Quand il a rejoint Léon, celui-ci a parcouru 100 m. Max rejoint Léon 50 s après avoir débuté sa course. vrai 7,2 km/h = 2 m/s ; Léon parcourt : 100 = 2 t soit t = 50 s ( durée de la course de Max) La vitesse de Max est vMax =2(1 + 2½) m/s. vrai t1 : durée de l'aller ; t2 :
durée du retour ; t1+ t2 = 50
(1) Max rattrape Jules 25 s après avoir quitté Léon. faux t1 =
100/(vMax-2)
=
100 / (2* 2½
) = 50 / 2½=
35,4 s.
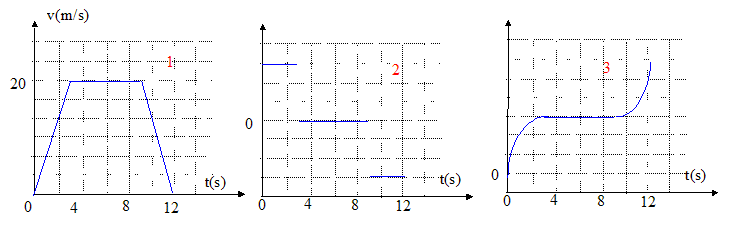
La figure 2 représente-t-elle l'accélération ? vrai. Le vecteur accélération est la dérivée par rapport au temps du vecteur vitesse. entre 0 et 3 s : la vitesse est une fonction linéaire croissante, son coefficient directeur, donc la valeur de l'accélération, est positif. entre 3 et 9 s : la vitesse est constante ; donc l'accélération est nulle. entre 9 et 12 s : la vitesse est une fonction affine décroissante, son coefficient directeur, donc la valeur de l'accélération est négative. Donc le graphe 2 représente l'accélération. La figure 3 représente -t-elle la distance parcourue ? non. La distance est une de la vitesse. entre 0 et 3 s : v= 20/3 t ; distance parcourue D1 = ½ 20/3 t² = 10/3 t² ( branche de gauche, la concavité devrait être vers le haut ) entre 3 et 9 s : v= 20 m/s : distance parcourue D2 = 20 t ( fonction affine croissante et non pas constante comme sur le graphe 3) entre 9 et 12 s : v= -20/3 t ; distance parcourue D3 = 10/3 t² ( branche de parabole, la concavité devrait être vers le bas). Donc le graphe 3 de convient pas. Les vecteurs accélération et vitesse sont-ils toujours orientés dans le même sens ? non. Vecteurs accélération et vitesse sont colinéaires : de même sens entre 0 et 3 s : la vitesse augmente de sens contraire entre 9 et 12 s : la vitesse diminue. Le mobile fait-il demi-tour à t= 9 s ? non. A partir de t= 9 s, la vitesse diminue et le mobile s'arrète à t = 12 s. Avant de faire demi-tour il faut d'abord s'arrêter : à t= 9 s, il n'y a pas d'arrêt ( vitesse non nulle) , et donc pas de demi-tour. Le mobile parcourt-il 180 m en 12 s ? vrai. D1 = 10/3*3² = 30 m D2 = 20*(9-3)= 120 m D3 = D1 = 30 m distance parcourue : 180 m. |
||||||||
|
|
||||||||
|
|